Build Your Own Z80 Computer: A Classic Guide to DIY Microcomputing
In 1981, Steve Ciarcia published what would become one of the most influential books in the homebrew computing movement: Build Your Own Z80 Computer: Design Guidelines and Application Notes. Published by BYTE Books, this comprehensive guide took readers on a journey from understanding basic power supply design all the way through constructing a fully functional microcomputer called ZAP (Z80 Applications Processor). More than four decades later, the book remains a fascinating window into an era when building your own computer wasn't just possible—it was expected.

The Author and His Mission
Steve Ciarcia was already well-known to readers of BYTE magazine through his popular "Ciarcia's Circuit Cellar" column, where he regularly presented do-it-yourself hardware projects. His columns had generated substantial reader interest, revealing that despite the growing availability of assembled personal computers, there remained a dedicated community of technically-minded individuals who wanted to understand what was inside their machines—and build them themselves.
Ciarcia wrote in the introduction: "Build Your Own Z80 Computer is a book written for technically minded individuals who are interested in knowing what is inside a microcomputer. It is for persons who, already possessing a basic understanding of electronics, want to build rather than purchase a computer."
This wasn't a book for beginners who had never held a soldering iron, nor was it an engineering textbook filled with impenetrable mathematics. Ciarcia positioned it squarely in the middle—practical enough for the determined hobbyist, technical enough to provide genuine understanding.
The book also reflected Ciarcia's pragmatic philosophy about engineering design. He shared an anecdote about having lunch with the designer of a major personal computer system, expecting to hear about months of careful optimization and instruction set analysis. Instead, he learned the designer had simply been given two months to produce something manufacturable, and had built the system around the microprocessor he happened to already own. "So much for textbook engineering design," Ciarcia noted wryly, while acknowledging that hobbyists doing hand-wiring needed to be more deliberate in their choices.
Why the Z80?
The choice of the Z80 microprocessor as the heart of the ZAP computer wasn't arbitrary. Ciarcia explained that when building a microcomputer from scratch, several criteria must be carefully considered: circuit complexity, cost, and software compatibility.
The Z80 (also available in 5-packs), introduced by Zilog in 1976, offered a compelling combination of features. It executed the complete instruction set of the Intel 8080A while adding significant enhancements of its own. Where the 8080A required multiple support chips (the 8224 clock driver and 8228 bus controller) to function, the Z80 integrated much of this functionality on-chip. This meant fewer components, simpler wiring, and reduced opportunities for errors—critical considerations for hand-wired projects.

The Z80's architecture included 158 instructions (compared to the 8080A's 78), dual register sets for rapid context switching, index registers for sophisticated addressing modes, and a built-in memory refresh counter for dynamic RAM. The processor came in a standard 40-pin dual inline package, with clearly defined buses: a 16-bit address bus capable of addressing 64K bytes of memory, an 8-bit bidirectional data bus, and a comprehensive control bus.
Ciarcia also noted the practical reality of the personal computer market: "The fact that so many personal computers are in use has established de facto standardization of central processor choice." The Z80 was already powering popular systems like the TRS-80, Sinclair ZX80, and numerous CP/M machines, which meant abundant software and documentation were available.
The Z80 compared favorably to its contemporaries. While the Motorola 6800 and MOS Technology 6502 were capable processors, Ciarcia's analysis considered three key factors: circuit complexity (keeping components to a minimum to reduce wiring errors), cost (finding the sweet spot between cheap discrete logic and expensive LSI), and software compatibility (ensuring the user could benefit from existing programs and development tools). The Z80 struck an optimal balance across all three dimensions for the hand-wired builder.
Starting With the Power Supply
In a decision that reveals much about Ciarcia's pedagogical approach, the book begins not with the glamorous central processor but with the humble power supply. His reasoning was both practical and psychological: "This is a good way to test ability and provide immediate positive reinforcement from successful construction."
The ZAP computer required three DC voltage rails: +5V at 5 amps for the digital logic, and ±12V at 1 amp each for peripheral interfaces and analog circuits. Ciarcia devoted an entire chapter to power supply design, explaining transformer selection, full-wave bridge rectification, filter capacitor sizing, and three-terminal voltage regulators.
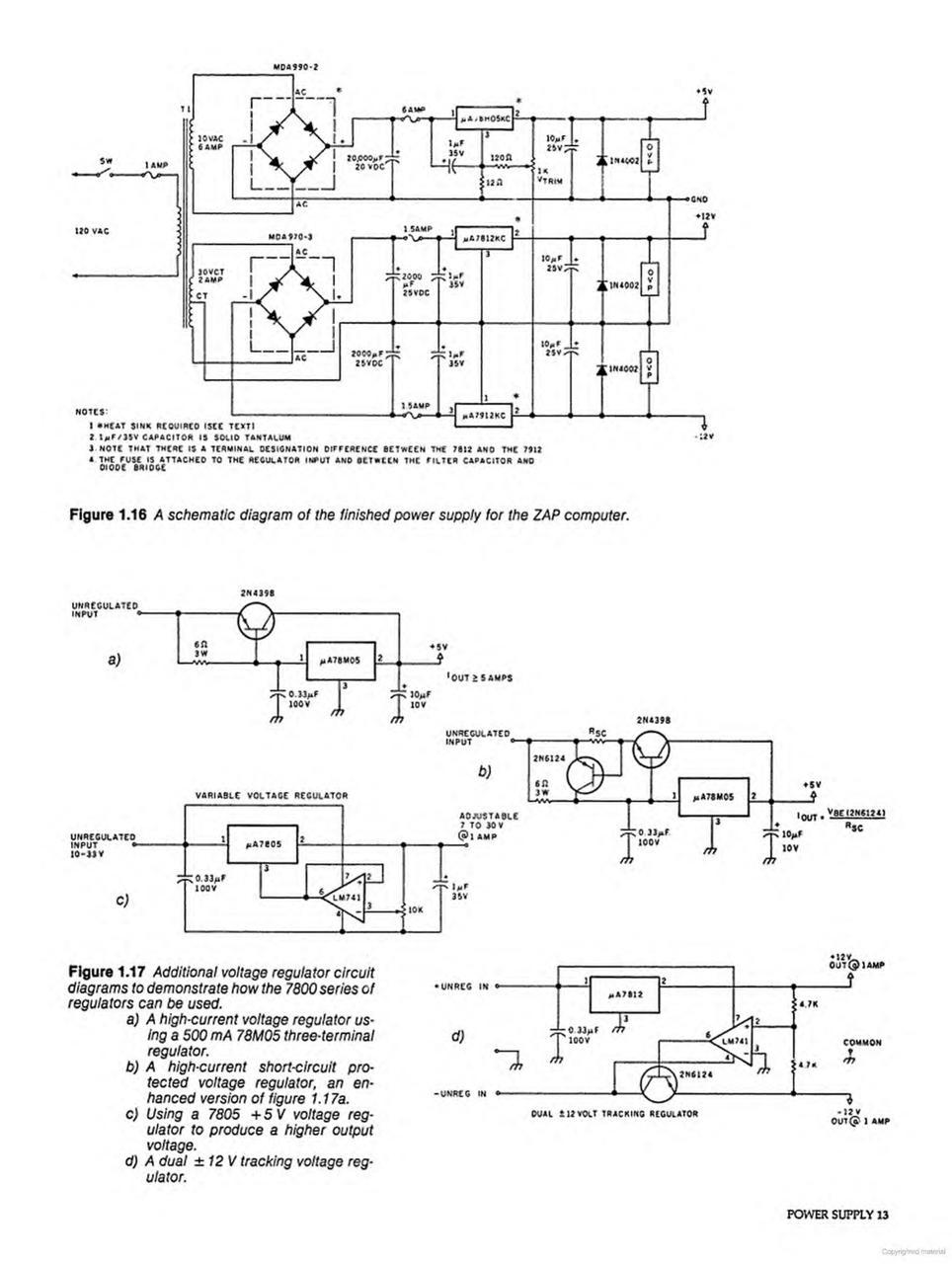
The technical depth here is remarkable. Readers learned about ripple voltage calculations, the relationship between peak voltage and steady-state voltage, and why a 25% ripple factor was recommended for the filter capacitor. The explanation of three-terminal regulators like the μA78H05 covered not just their use but their internal operation—bandgap references, error amplifiers, and thermal protection circuits.
Perhaps most valuably, Ciarcia addressed overvoltage protection. Recognizing that a regulator failure could send dangerous voltage spikes to sensitive logic circuits, he included detailed designs for SCR-based "crowbar" circuits that would short the output to ground and blow a fuse before damage could occur. This wasn't theoretical paranoia—it was the kind of practical wisdom that came from experience with real-world failures.
The chapter also tackled thermal management—a subject often glossed over in hobbyist literature. Ciarcia explained heat sink calculations, thermal resistance from junction to ambient, and the importance of forced air cooling for high-current regulators. His advice was characteristically practical: "I hate red-hot power supplies." Rather than agonize over precise thermal calculations, he recommended adequate heat sinking combined with a fan. The additional cost of robust cooling was, he noted, far less than the cost of replacing fried computer components.
Layout considerations received equal attention. Ciarcia explained how improper placement of filter capacitors could induce ripple on the output voltage, and how resistance in power distribution wiring could create different voltage levels at different points in the circuit. His solution—heavy gauge wire, single-point grounding, and dedicated bus strips—reflected the kind of hard-won practical knowledge that separates reliable designs from troublesome ones.
Understanding the Z80's Internal Architecture
Chapter 3 provides what amounts to a complete Z80 programmer's reference. Ciarcia walked through every aspect of the processor's architecture: the accumulator and flag registers, general-purpose register pairs (BC, DE, HL), special-purpose registers (program counter, stack pointer, index registers IX and IY), and the interrupt and refresh registers.
The dual register set architecture received particular attention. The Z80 contained two complete sets of general-purpose registers—main and alternate—that could be swapped with single exchange instructions. This feature enabled rapid interrupt handling and context switching, capabilities that made the Z80 attractive for real-time applications.
The instruction set documentation is exhaustive—rivaling dedicated references like Rodnay Zaks' Programming the Z80 (PDF) and Ramesh Gaonkar's The Z80 Microprocessor: Architecture, Interfacing, Programming and Design. Every instruction is described with its mnemonic, operation, affected flags, byte encoding, cycle count, and timing states. Load and exchange instructions, arithmetic and logical operations, block transfer and search commands, rotate and shift operations, bit manipulation, jumps, calls, returns, and I/O instructions—all are covered with the detail needed for hand assembly of machine code.
Ciarcia also explained the hardware interface: the meaning of every pin on the Z80's 40-pin package. Control signals like MREQ (memory request), IORQ (I/O request), RD (read), WR (write), and RFSH (refresh) are described in terms of their logical function and timing relationships. The interrupt system, with its three modes and maskable/non-maskable hierarchy, receives thorough treatment.
Building the Basic Computer
Chapter 4, "Build Your Own Computer—Start With the Basics," transitions from theory to practice. The approach is methodical: construct the minimum viable system first, verify its operation, then expand.
The basic ZAP configuration included the Z80 processor, 1K of EPROM containing the monitor program, 2K of static RAM for user programs and stack, address decoding logic, and a hexadecimal display with keyboard for interaction. Ciarcia deliberately avoided elaborate peripherals in the initial build, focusing instead on achieving a working foundation.
Memory architecture was a central concern. Ciarcia explained memory mapping—the allocation of the Z80's 64K address space among ROM, RAM, and I/O devices. For ZAP, the memory map placed the 1K monitor EPROM at addresses 0000-03FF (where the Z80 begins execution after reset), with RAM starting at address 2000 hex.
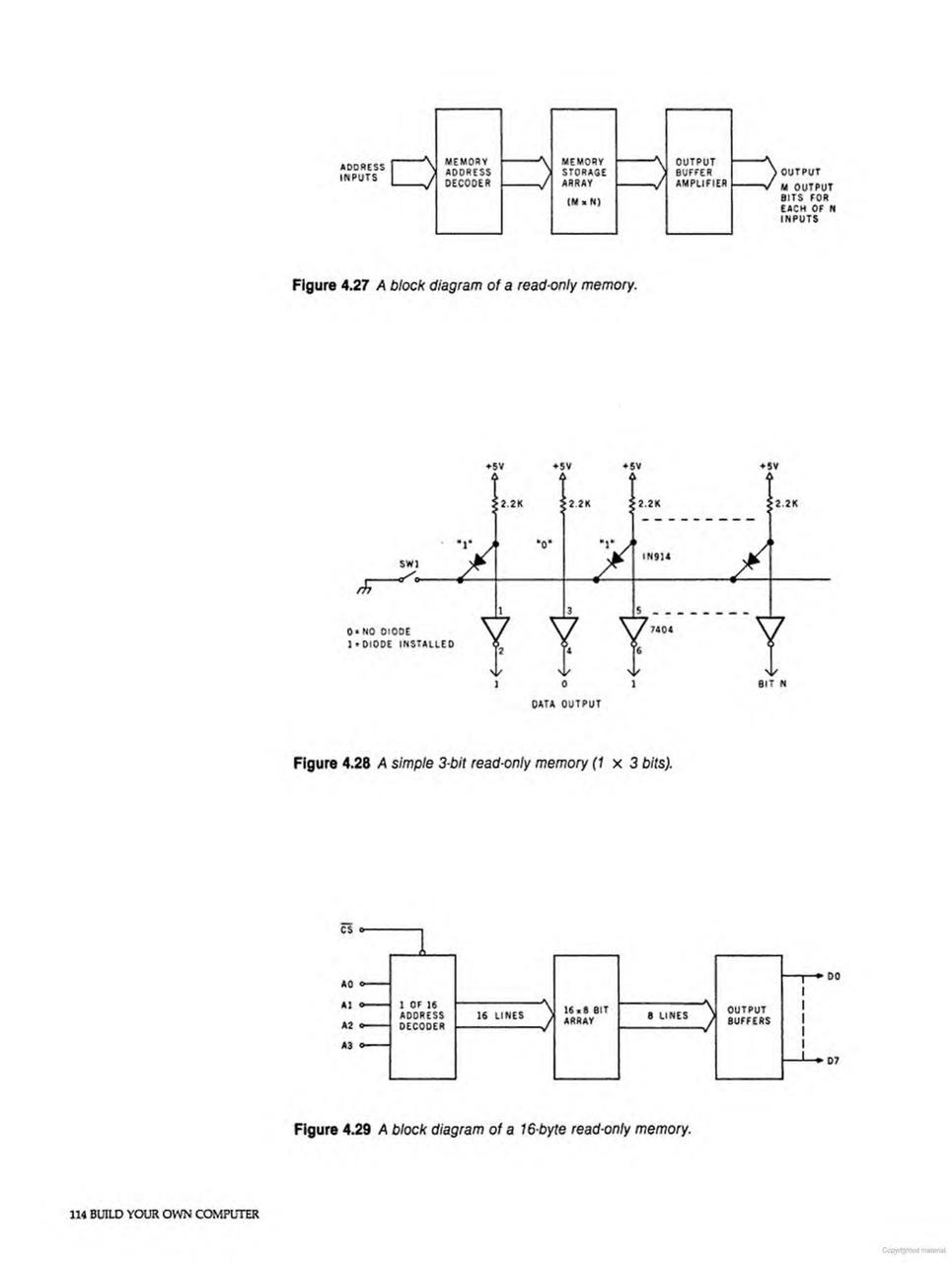
The discussion of memory devices compared available options. The 2716 EPROM (2K × 8) and 2114 static RAM (1K × 4) were recommended for their balance of capacity, availability, and ease of use. Ciarcia explained why static RAM was preferred over dynamic RAM for this application—dynamic RAM required refresh logic that, while supported by the Z80, added complexity inappropriate for a learning project.
Address decoding used simple 74LS138 three-to-eight decoders, with higher address lines selecting among memory banks and lower lines addressing within each device. This straightforward approach traded some address space efficiency for wiring simplicity.
The Peripheral Ecosystem
With the basic computer operational, Chapter 5 expanded the system with practical peripherals. The hexadecimal display and keyboard provided the most basic human interface, allowing users to examine and modify memory contents, run programs, and debug code.
The RS-232C serial interface opened connections to terminals and other equipment. Ciarcia used the COM2017 UART (Universal Asynchronous Receiver/Transmitter) to handle serial data formatting, baud rate generation, and handshaking. The interface supported standard rates from 110 to 9600 baud, making ZAP compatible with widely available terminals.
For mass storage, the book included a cassette interface design. In 1981, audio cassettes were the affordable mass storage medium for personal computers. Ciarcia's design used the Kansas City Standard (300 baud), encoding data as audio tones that could be recorded on any audio cassette recorder. While primitive by modern standards, this approach made program storage accessible without expensive disk drives.
The ZAP Monitor Software
Chapter 6 revealed the software that breathed life into the hardware. The ZAP monitor was a 1K program stored in EPROM that coordinated system operations and provided a command interface for the user.
The monitor's capabilities included: - Memory examination and modification - Program execution from specified addresses - Register display and modification - Block memory operations (move, fill, compare) - Cassette load and save operations - Breakpoint debugging support
Ciarcia presented the complete source code with detailed annotations. The listings served dual purposes: they documented the specific monitor implementation, and they provided extensive examples of Z80 assembly language programming. Readers learned about interrupt handling, I/O programming, data structure manipulation, and subroutine organization—not from abstract examples but from working, useful code.
The flow diagrams accompanying the source code illustrated program logic visually, a documentation technique that helped readers understand the relationships between code sections before diving into instruction-level details.
Programming an EPROM
Chapter 7 addressed a critical practical concern: how to get the monitor program into the EPROM in the first place. This chicken-and-egg problem—needing a programmed EPROM to have a working computer, but needing a working computer to program an EPROM—was solved through a dedicated EPROM programmer built as part of the ZAP system.
Ciarcia's EPROM programmer design could program 2708, 2716, and similar devices. The programming process required specific voltage sequences and timing, all explained in sufficient detail for readers to understand the underlying physics of EPROM operation. For those who preferred to avoid this bootstrap problem, Ciarcia noted that programmed EPROMs were available by mail order.
Connecting ZAP to the Real World
Chapter 8, "Connecting ZAP to the Real World," transformed the computer from an abstract digital machine into a practical tool for measurement and control. This chapter covered analog-to-digital and digital-to-analog conversion, enabling ZAP to interact with continuous physical quantities.
The A/D converter design used the ADC0804, an 8-bit successive approximation converter that could digitize analog signals for processing. Applications ranged from simple voltage measurement to data logging systems that could record environmental parameters over time.
On the output side, D/A conversion allowed ZAP to generate analog signals for control applications. Ciarcia included a particularly interesting application: digital speech synthesis using the SC-01 speech synthesizer chip. By sending phoneme codes from the Z80 to the speech chip, ZAP could produce intelligible spoken output—a capability that seemed almost magical in 1981.
Building a CRT Terminal
The final major project, Chapter 9, was arguably the most ambitious: a complete CRT terminal. Rather than connecting ZAP to an expensive commercial terminal, readers could build their own using the CRT5027 video timer/controller and CRT8002 video attributes controller.
The terminal design supported an 80-column by 24-row display—the standard format that would dominate computing for decades. Character generation used a ROM-based approach, with dot-matrix patterns for the full ASCII character set. The design included cursor control, scrolling, and basic display attributes.
This project integrated many skills developed earlier in the book: power supply design, digital logic, memory interfacing, and RS-232 communication. The completed terminal could serve not only ZAP but any computer with a serial port, making it a genuinely useful piece of equipment.
The terminal design included detailed worksheets for calculating timing parameters—horizontal and vertical sync widths, blanking intervals, and character clock rates. These calculations showed readers how video timing worked at a fundamental level, demystifying what seemed like magic to many hobbyists. The result was not just a working terminal but genuine understanding of raster-scan display technology.
The Appendices: Reference Material
The appendices transformed the book from a tutorial into a reference. Appendix A covered construction techniques—wire-wrapping, soldering, and printed circuit board fabrication. Appendix B provided ASCII code tables. Appendix C collected manufacturers' specification sheets for key components, eliminating the need to track down separate datasheets.
Appendix D contained the complete ZAP operating system listing, while Appendix E provided Z80 CPU technical specifications including electrical characteristics, timing diagrams, and the complete instruction set summary. The glossary and index made the book's wealth of information accessible for quick reference.
The Historical Context
To fully appreciate Build Your Own Z80 Computer, one must understand the computing landscape of 1981. The MITS Altair 8800 had kicked off the personal computer revolution just six years earlier. The Apple II was four years old. The Commodore PET and TRS-80 were both recent arrivals. Computing was still new enough that the question "Should I build or buy?" was legitimate.
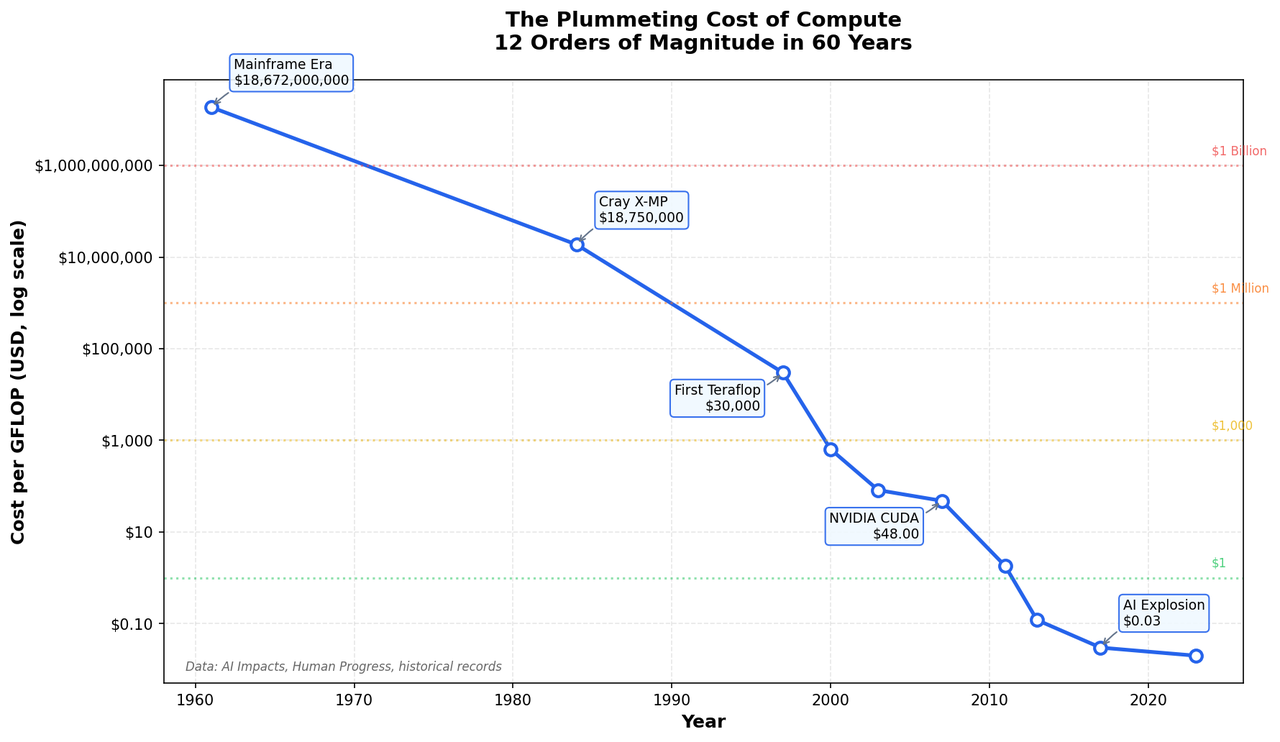
Commercial computers were expensive—often thousands of dollars—while components were relatively cheap. A skilled hobbyist with time could build substantial systems for a fraction of the commercial cost. More importantly, building your own computer meant you understood it completely. When something broke, you could fix it. When you wanted to expand it, you knew how. This self-reliance was both necessity and philosophy in the early hobbyist community.
The book also appeared during the golden age of electronics magazines. BYTE, Radio Electronics, Popular Electronics, and others featured monthly construction articles. Readers expected detailed schematics, parts lists, and construction notes. Ciarcia's book was, in many ways, an extended version of the magazine articles that had made him famous—but comprehensive enough to guide a reader through an entire computer system rather than a single peripheral.
The Book's Lasting Significance
Build Your Own Z80 Computer appeared at a transitional moment in computing history. The homebrew era of the mid-1970s, when building your own computer was often the only affordable option, was giving way to an era of mass-produced personal computers. The IBM PC would debut later in 1981, accelerating the shift toward standardized, commercially manufactured systems.
Yet Ciarcia's book served a purpose beyond mere necessity. It educated a generation of engineers and enthusiasts in the fundamentals of digital design. Readers who worked through ZAP gained deep understanding of computer architecture—not just how to use a computer, but how computers actually work at the hardware level. Many professional engineers who came of age in the 1980s cite this book—or Ciarcia's magazine columns—as formative influences on their careers.
The book also demonstrated that complex systems could be understood through systematic decomposition. By building each subsystem separately, testing it in isolation, and then integrating the pieces, even ambitious projects became manageable. This approach to complexity management remains relevant today, whether one is building embedded systems, designing software architectures, or troubleshooting network infrastructure.
The pedagogical approach Ciarcia employed—theory interspersed with practice, abstract concepts grounded in concrete examples—anticipated modern project-based learning. Readers weren't just told how a regulator worked; they built one and measured its performance. They weren't just taught about memory addressing; they wired decode logic and watched the computer access specific memory locations. This hands-on approach created understanding that mere reading could never provide.
For the retrocomputing enthusiast, Build Your Own Z80 Computer offers both historical insight and practical guidance. The Z80 remains available, its instruction set unchanged from 1976. Modern implementations on FPGAs and emulators keep the architecture accessible. Projects like the RC2014 and other Z80-based single-board computers carry forward the tradition of building your own system. For those inspired to design their own Z80 system from scratch, J.S. Walker's Design a Z80 Computer provides a modern practical guide to discrete-logic computer design. And Ciarcia's thorough documentation makes it possible to understand—and even construct—systems that defined the early personal computer era.
Steve Ciarcia went on to found Circuit Cellar magazine and continued contributing to the hobbyist electronics community for decades. But Build Your Own Z80 Computer remains perhaps his most complete and influential work—a comprehensive guide that took readers from bare components to working computer, explaining every step along the way.
The book stands as a testament to an era when understanding technology meant building it yourself, one wire at a time. In an age of sealed devices and cloud computing, there's something deeply satisfying about returning to first principles—about understanding that a computer is ultimately just silicon responding to voltages, executing instructions one cycle at a time, exactly as Steve Ciarcia explained over four decades ago.