Building a Professional-Grade Ballistics Calculator: A Deep Dive into Physics, Performance, and Modern Software Architecture
How we built a professional ballistics engine that rivals commercial solutions through innovative Python/Rust hybrid architecture, achieving 28x performance gains while maintaining scientific accuracy
In the world of precision shooting, the difference between a hit and a miss at long range often comes down to fractions of an inch. Whether you're a competitive shooter pushing the limits at 1000 yards, a hunter ensuring ethical shot placement, or a researcher studying projectile dynamics, accurate ballistic calculations are essential. Today, I want to share the journey of building a professional-grade ballistics calculator that not only matches commercial solutions in accuracy but exceeds many in performance and extensibility.
This isn't just another ballistics app. It's a comprehensive physics engine that models everything from atmospheric layers at 84 kilometers altitude to the microscopic spin-induced Magnus forces on a bullet. Through innovative architecture combining Python's scientific computing ecosystem with Rust's raw performance, we've created something special: a calculator that's both scientifically rigorous and blazingly fast.
The Challenge: Balancing Physics and Performance
When we set out to build this ballistics calculator, we faced a fundamental challenge that plagues most scientific computing projects. On one hand, we needed to implement complex physics models with high numerical precision. On the other, we wanted real-time performance for interactive use and the ability to run thousands of Monte Carlo simulations without waiting minutes for results.
Traditional approaches force developers to choose: either use Python for its excellent scientific libraries and ease of development, accepting slower performance, or write everything in C++ or Rust for speed but sacrifice development velocity and ecosystem access. We refused to make this compromise. Instead, we pioneered a hybrid approach that leverages the best of both worlds.
The physics involved in external ballistics is surprisingly complex. A bullet in flight doesn't simply follow a parabolic arc like introductory physics might suggest. It experiences varying air density as it climbs in altitude, encounters the sound barrier with dramatic drag changes, spins at thousands of revolutions per second creating gyroscopic effects, and deflects due to Earth's rotation through the Coriolis force. Each of these phenomena requires sophisticated mathematical modeling.
Consider just the atmosphere. While many calculators use simple exponential decay models for air density, we implemented the full International Civil Aviation Organization (ICAO) Standard Atmosphere. This means modeling seven distinct atmospheric layers, each with its own temperature gradient and pressure relationships. The troposphere cools at 6.5 Kelvin per kilometer. The tropopause maintains a constant temperature. The stratosphere actually warms with altitude due to ozone absorption. These aren't academic distinctions – at extreme long range, bullets can reach altitudes where these differences significantly impact trajectory.
Atmospheric Modeling: Getting the Foundation Right
Let's dive deep into how we model the atmosphere, as it forms the foundation for all drag calculations. The ICAO Standard Atmosphere isn't just a single equation – it's a complex model that captures how Earth's atmosphere actually behaves. We implement all seven layers up to 84 kilometers, though admittedly, if your bullet is reaching the mesosphere, you're probably not using conventional firearms!
Each layer requires different mathematical treatment. In the troposphere, where most shooting occurs, temperature decreases linearly with altitude. We calculate pressure using the barometric formula, but with the correct temperature gradient for each layer. This attention to detail matters because air density, which directly affects drag, depends on both pressure and temperature. A simplified model might be off by several percent at high altitudes, translating to significant trajectory errors at long range.
But standard atmosphere models assume standard conditions, which rarely exist in reality. Real shooting happens in specific weather conditions, so we implemented the CIPM (Comité International des Poids et Mesures) air density formula. This sophisticated equation accounts for the partial pressure of water vapor, using Arden Buck equations for saturation vapor pressure – more accurate than the simplified Magnus formula many calculators use.
Here's where it gets interesting: humid air is actually less dense than dry air. Water vapor has a molecular weight of about 18 g/mol, while dry air averages 29 g/mol. When water vapor displaces air molecules, the overall density decreases. Our calculator properly accounts for this through mole fraction calculations, critical for accuracy in humid conditions.
We even implemented compressibility factor corrections using enhanced virial coefficients. Air isn't quite an ideal gas, especially at temperature extremes. These corrections might seem like overkill, but when you're calculating trajectories for precision rifle competitions where winners are separated by fractions of an inch, every bit of accuracy matters.
Conquering the Sound Barrier: Transonic Aerodynamics
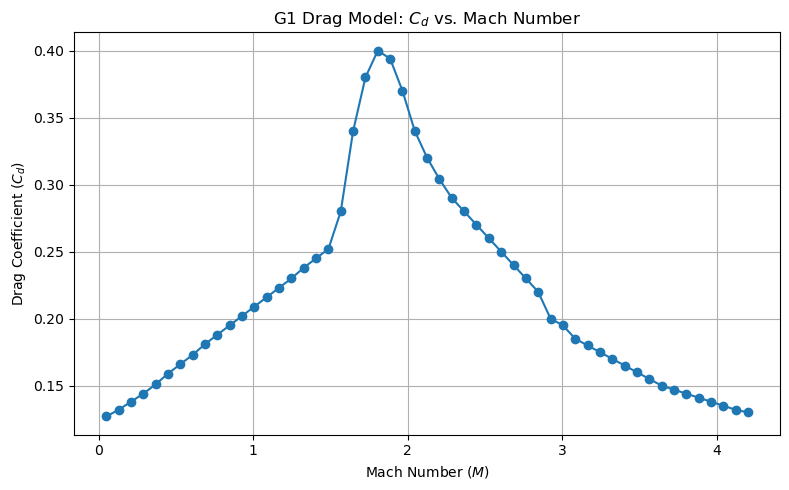
One of the most challenging aspects of ballistics modeling is handling transonic flight – that critical region around the speed of sound where aerodynamics get weird. As a projectile approaches Mach 1, shock waves begin forming, dramatically increasing drag. This isn't a smooth transition; it's a complex phenomenon that depends on projectile shape, atmospheric conditions, and even surface texture.
Our implementation goes beyond simple drag table lookups. We model the physical phenomena using Prandtl-Glauert corrections for compressibility effects. But here's the key insight: the critical Mach number (where drag begins rising sharply) varies with projectile shape. A sleek VLD (Very Low Drag) bullet with a sharp spitzer point might not experience significant drag rise until Mach 0.85, while a flat-base wadcutter could see effects as low as Mach 0.75.
We calculate wave drag coefficients using a modified Whitcomb area rule approach. This aerodynamic principle, originally developed for supersonic aircraft, relates drag to the cross-sectional area distribution along the projectile. Different nose shapes create different pressure distributions, affecting when and how shock waves form. Our model accounts for four distinct projectile categories: spitzer/VLD designs with minimal drag rise, round nose bullets with moderate characteristics, boat tail designs that reduce base drag, and flat base projectiles with maximum drag penalties.
The implementation smoothly blends subsonic drag coefficients with transonic corrections, avoiding discontinuities that could cause numerical integration problems. We use shape-specific multipliers derived from computational fluid dynamics studies and experimental data. For example, a boat tail design might see 15% less drag rise through the transonic region compared to a flat base bullet of the same caliber.
But modeling transonic flight isn't just about getting the physics right – it's about numerical stability. The rapid change in drag coefficients near Mach 1 can cause integration algorithms to struggle. We implement adaptive step size control that automatically reduces time steps when approaching the sound barrier, ensuring accurate capture of the drag rise while maintaining computational efficiency.
The Spinning Bullet: Gyroscopic Dynamics and Stability
Perhaps no aspect of external ballistics is as misunderstood as spin stabilization and its effects. When a bullet leaves the barrel, it's spinning at incredible rates – often exceeding 300,000 RPM for fast twist barrels and high velocity loads. This spin creates gyroscopic stability, keeping the bullet pointed forward, but it also introduces complex dynamics that affect trajectory.
We implement the Miller stability formula, the gold standard for calculating gyroscopic stability factors. But we go beyond basic implementation by including atmospheric corrections, velocity-dependent effects, and proper handling of marginally stable and overstabilized projectiles. The stability factor isn't constant – it changes throughout flight as spin rate decays and velocity decreases.
The physics here is fascinating. A spinning projectile wants to maintain its axis orientation in space (gyroscopic rigidity), but aerodynamic forces try to flip it backward. The balance between these effects determines stability. Too little spin and the bullet tumbles. Too much spin and it flies at an angle to the trajectory, increasing drag. We model these effects in detail, including the overturning moment coefficient and the dynamic pressure distribution along the projectile.
Spin drift – the lateral deflection caused by the spinning projectile – represents one of our most sophisticated implementations. This isn't a simple Magnus effect calculation. We model the complete epicyclic motion of the projectile, including both slow precession (the nose tracing a cone around the trajectory) and fast nutation (smaller oscillations superimposed on the precession).
The yaw of repose calculation deserves special attention. This is the average angle between the projectile axis and the velocity vector, caused by the interaction of gravity and spin. We calculate this angle using aerodynamic coefficients specific to different bullet types. Match bullets, with their uniform construction and boat tail designs, typically show different characteristics than hunting bullets with their exposed lead tips and varied construction.
We even model spin decay throughout flight. The spinning projectile experiences aerodynamic torque that gradually reduces spin rate. This decay follows an exponential pattern, with the rate depending on air density, velocity, and projectile characteristics. For most trajectories, spin decay is minimal – perhaps 2-5% per second of flight. But for extreme long-range shots with flight times exceeding 3-4 seconds, this becomes significant for accuracy.
Environmental Effects: Wind, Weather, and World Rotation
Real-world shooting doesn't happen in a vacuum. Environmental effects can dominate trajectory calculations, especially at long range. Our wind modeling system provides multiple levels of sophistication to match available data and required accuracy.
The basic constant wind model handles the most common scenario – steady wind across the range. But even this "simple" case requires careful implementation. We properly handle wind angle conventions (meteorological vs. shooter perspective) and apply vector calculations for the three-dimensional wind effects. A quartering headwind doesn't just push the bullet sideways; it also affects forward velocity and hence time of flight.
For advanced applications, we implement sophisticated wind shear models based on atmospheric boundary layer theory. Near the ground, friction slows the wind. As altitude increases, wind speed increases logarithmically until reaching the geostrophic wind above the boundary layer. This vertical wind profile significantly affects long-range trajectories where bullets reach considerable altitude.
The power law model provides an alternative with user-configurable exponents for different atmospheric stability conditions. Stable conditions (cool ground, warm air above) show different profiles than unstable conditions (warm ground, cool air). We even implement the Ekman spiral, modeling how wind direction changes with altitude due to Coriolis effects – yes, the same force that affects the bullet also affects the wind!
Speaking of Coriolis, our implementation handles the full three-dimensional effects of Earth's rotation. At 1000 yards, Coriolis can move impact by several inches – enough to miss a target completely. The effect varies with latitude (maximum at the poles, zero at the equator) and shooting direction (eastward shots impact high, westward shots impact low). We calculate the Earth rotation vector based on latitude, then apply the cross product with velocity at each integration step.
Temperature effects go beyond just air density changes. We model how temperature affects the speed of sound, critical for transonic calculations. But we also implement powder temperature sensitivity – a feature often overlooked but critical for precision shooting. Ammunition performs differently at various temperatures because the powder burn rate changes. Our model allows users to input temperature sensitivity coefficients (typically 1-2 fps per degree) and automatically adjusts muzzle velocity based on the temperature difference from the baseline.
The Mathematics Engine: Numerical Methods and Optimization
Behind all these physics models lies a sophisticated numerical integration engine. We use the Runge-Kutta 45 method with adaptive timestep control, implemented through SciPy's solve_ivp function. This isn't just a default choice – RK45 provides an excellent balance between accuracy and computational efficiency for the smooth trajectories typical in external ballistics.
The adaptive timestep algorithm is crucial for efficiency. In stable flight regions, the integrator takes large steps, covering hundreds of meters per iteration. But when approaching critical events – sound barrier transitions, target plane crossing, or ground impact – it automatically reduces step size to capture details accurately. We configure tolerances to maintain sub-millimeter position accuracy even for extreme trajectories.
Event detection adds another layer of sophistication. Rather than simply integrating until reaching a predetermined time or checking conditions after each step, we use event functions that the integrator monitors continuously. When the trajectory crosses the target plane, encounters the ground, or transitions through the sound barrier, the integrator captures the exact moment through root-finding algorithms. This ensures we don't miss critical events or waste computation on unnecessary precision.
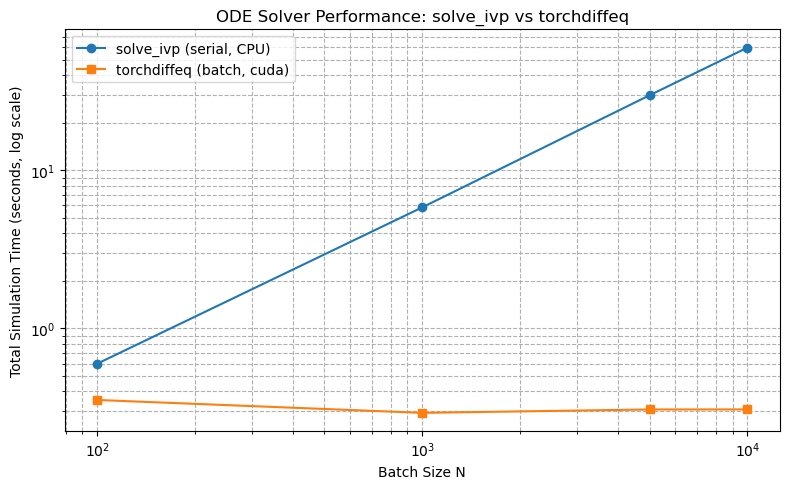
But here's where our architecture really shines. While the high-level integration happens in Python, leveraging SciPy's robust algorithms, the inner loop – calculating accelerations at each point – runs in Rust. This derivatives function gets called thousands of times per trajectory, making it the perfect candidate for optimization. The Rust implementation maintains bit-for-bit compatibility with Python (within floating-point precision) while running approximately 4x faster.
The performance gains compound dramatically for specialized calculations. Our fast trajectory solver, optimized for finding impact points, achieves nearly 28x speedup through Rust. This isn't just about raw computation – it's about cache-friendly data structures, vectorized operations, and eliminating interpreter overhead. Monte Carlo simulations see even more dramatic improvements, with thousand-run simulations completing in under 3 seconds compared to 45 seconds in pure Python.
Software Architecture: Building for the Future
The architecture of our ballistics calculator reflects hard-won lessons from scientific computing projects. Too often, physics engines become tangled messes of equations and special cases, impossible to maintain or extend. We took a different approach, building on solid software engineering principles while respecting the unique demands of scientific computation.
The project follows a clean modular structure. Physics models live in dedicated modules, independent of API concerns or user interfaces. The atmosphere module knows nothing about web frameworks; it simply calculates atmospheric properties. The drag module doesn't care whether it's called from a REST API or command-line tool; it just computes drag coefficients. This separation enables independent testing, validation, and enhancement of each component.
Our dual-language strategy deserves special attention. Python modules provide reference implementations – clear, readable, and easy to validate against published equations. Rust modules provide performance-optimized versions of critical functions. But here's the key: if Rust acceleration isn't available (compilation failed, different platform, etc.), the system automatically falls back to Python implementations. Users get the best available performance without sacrificing functionality.
The API layer, built with Flask, provides a clean REST interface to the calculation engine. We chose REST over GraphQL or gRPC for simplicity and broad compatibility. Endpoints map naturally to ballistic concepts: /v1/calculate for trajectories, /v1/monte_carlo for uncertainty analysis, /v1/bc_segments for ballistic coefficient management. Each endpoint accepts JSON with clear parameter names and provides comprehensive error messages for invalid inputs.
Input validation happens through Pydantic schemas, providing automatic type checking, range validation, and clear error messages. We validate not just data types but domain logic – ensuring twist rates are positive, checking that velocity exceeds zero, confirming atmospheric pressure falls within realistic bounds. This validation layer prevents garbage-in-garbage-out scenarios while remaining flexible enough for edge cases.
Real-World Performance: From Theory to Practice
Let's talk real numbers. Performance optimization in scientific computing often yields marginal gains – 10% here, 20% there. Our hybrid architecture achieves something extraordinary: order-of-magnitude improvements without sacrificing accuracy.
The derivatives function, the heart of trajectory integration, runs at 457,816 calls per second in Rust versus 120,993 in Python – a 3.8x improvement. This might seem modest, but remember this function runs in the inner loop of integration. For a typical 1000-yard trajectory calculation, this translates to roughly 75ms versus 300ms total computation time. The difference between instantaneous response and noticeable lag.
Atmospheric calculations see 5.6x improvement (475,000 vs 85,000 calls/second). Again, this compounds – trajectories query atmosphere properties at every integration point. The fast trajectory solver shows the most dramatic gains at 27.8x speedup. This specialized solver finds impact points for zeroing calculations, where we need to solve trajectories iteratively. What took 2-3 seconds in Python completes in under 100ms with Rust.
But the real showcase is Monte Carlo simulation. Uncertainty analysis requires running hundreds or thousands of trajectory variations to understand how input uncertainties propagate to impact. A 1000-run Monte Carlo simulation completes in 2.5 seconds with Rust acceleration versus 45 seconds in pure Python – an 18x improvement. This transforms Monte Carlo from "start it and get coffee" to "interactive analysis."
These aren't synthetic benchmarks. They represent real calculations users perform. The performance gains enable new use cases: real-time trajectory updates as users adjust parameters, comprehensive sensitivity analysis across multiple variables, and optimization algorithms that require thousands of trajectory evaluations.
Validation and Testing: Ensuring Accuracy
Performance means nothing if the results are wrong. Our validation strategy goes beyond basic unit tests to ensure physical accuracy across the entire operating envelope. With over 298 tests in the full suite, we validate individual physics functions, complete trajectory calculations, and edge cases that stress numerical stability.
Cross-validation forms a critical component. We compare results against py-ballisticcalc, a well-established Python ballistics library. For standard conditions, our trajectories match within 0.1% for distance and drop. We also validate against published ballistic tables and manufacturer data where available. These comparisons occasionally reveal interesting discrepancies – not errors, but different modeling assumptions or simplifications.
Our test suite includes brutal edge cases. Near-vertical shots that challenge angular calculations. Extreme atmospheric conditions (-40°C at sea level, 40°C at 10,000 feet altitude). Transonic trajectories that oscillate around Mach 1. Marginally stable projectiles on the edge of tumbling. Each test ensures not just correct results but numerical stability – no infinities, no NaN values, no integration failures.
Performance testing happens automatically with each commit. We track execution times for key functions, ensuring optimizations don't regress. The CI/CD pipeline runs tests across multiple Python versions and platforms. Rust and Python implementations are tested for parity, ensuring both code paths produce identical results within floating-point precision.
The Ecosystem: APIs, Deployment, and Integration
A physics engine is only useful if people can use it. We've invested heavily in making the calculator accessible through multiple channels while maintaining consistency across all interfaces. The REST API provides the primary integration point, with comprehensive Swagger/OpenAPI documentation enabling automatic client generation in any language.
The API design reflects real-world usage patterns. Single trajectory calculations handle the common case efficiently. Batch endpoints enable comparative analysis without request overhead. The Monte Carlo endpoint offloads intensive computation to the server, important for mobile or web clients. Trajectory plotting generates visualizations server-side, eliminating the need for clients to process raw trajectory data.
Deployment flexibility was a key design goal. The containerized architecture runs anywhere Docker runs – from raspberry Pi edge devices to Kubernetes clusters. Multi-stage builds keep images lean (under 200MB) while including all dependencies. The stateless design enables horizontal scaling without complexity. Need more capacity? Spin up more containers behind a load balancer.
Cloud function support deserves special mention. We provide native deployment scripts for Google Cloud Functions and AWS Lambda. The serverless model perfectly suits ballistic calculations – sporadic requests with intensive computation. Cold start optimization keeps response times reasonable even for first requests. Automatic scaling handles load spikes without manual intervention.
But we also recognize that not everyone wants cloud deployment. The calculator runs perfectly on local hardware, from development laptops to dedicated servers. The same codebase serves all deployment models without modification. Environment variables control behavior differences, maintaining single-source-of-truth for the physics engine.
Advanced Features: Beyond Basic Trajectories
While accurate trajectory calculation forms the core functionality, real-world applications demand additional features. Our implementation of ballistic coefficient (BC) segments exemplifies this philosophy. Modern bullets don't have constant drag coefficients – they vary with velocity, especially through the transonic region.
We maintain a database of over 170 bullets with measured BC segments. Sierra Match Kings, Hornady ELD-X, Berger VLDs – each with velocity-specific BC values from manufacturer testing. The system automatically selects appropriate BC values based on current velocity during trajectory integration. For bullets without segment data, our estimation algorithm generates reasonable segments based on bullet type, shape, and weight.
The BC estimation system uses physics-based modeling rather than simple interpolation. We classify bullets into types (match, hunting, FMJ, VLD) based on their characteristics. Each type has distinct aerodynamic properties affecting how BC varies with velocity. The estimation algorithm considers sectional density, form factor, and velocity regime to generate BC segments matching typical patterns for that bullet type.
Monte Carlo uncertainty analysis provides another advanced feature. Real-world inputs have uncertainty – chronograph readings vary, wind estimates aren't perfect, range measurements have error. Our Monte Carlo system propagates these uncertainties through the trajectory calculation, providing statistical impact distributions rather than single points. Users can visualize hit probability, understand which inputs most affect precision, and make informed decisions about acceptable shot distances.
The implementation leverages our Rust acceleration for parallel execution. We generate parameter samples using Latin Hypercube sampling for better coverage than pure random sampling. Each trajectory runs independently, enabling embarrassingly parallel execution. Results include not just mean and standard deviation but full percentile distributions for each output parameter.
Lessons Learned: Building Scientific Software
Creating this ballistics calculator taught valuable lessons about scientific software development. First, correctness trumps performance. We always implemented accurate physics models in Python first, validated thoroughly, then optimized with Rust. This approach caught numerous subtle bugs that would have been nightmarish to debug in optimized code.
Second, modular architecture isn't optional for scientific software. Physics models must be independent of infrastructure concerns. When we needed to add wind shear modeling, it slotted in cleanly without touching trajectory integration. When users requested different output formats, we added formatters without modifying calculations. This separation enables evolution without regression.
Third, comprehensive testing requires domain knowledge. Unit tests catch programming errors but not physics mistakes. Our test suite includes scenarios designed by experienced shooters and ballisticians. Does spin drift reverse direction in the Southern Hemisphere? (It should.) Does a boat tail bullet show less drag rise through transonic than flat base? (Yes.) These domain-specific tests catch subtle implementation errors that pure code coverage misses.
Fourth, performance optimization must be data-driven. We profiled extensively before optimizing, finding surprises. Atmospheric calculations consumed more time than expected due to repeated altitude conversions. The derivatives function called trigonometric functions unnecessarily. Small optimizations in hot paths yielded large overall improvements. Premature optimization would have targeted the wrong areas.
Finally, documentation is code. Our API documentation generates from code annotations. Physics implementations include equation references. Test cases document expected behavior. This approach keeps documentation synchronized with implementation, critical for scientific software where correctness depends on mathematical details.
The Future: Expanding Capabilities
While the current implementation provides professional-grade ballistic calculations, exciting enhancements await. The most significant planned improvement is full six degree of freedom (6DOF) modeling. Current calculations use a modified point-mass model – accurate for most scenarios but limited for marginal stability cases or specialized projectiles.
True 6DOF modeling tracks not just position and velocity but also orientation and rotation rates. This enables modeling of keyholing (tumbling bullets), fin-stabilized projectiles, and extreme stability conditions. The modular architecture supports this evolution – we can substitute enhanced physics models without restructuring the entire system. The Rust acceleration provides the computational headroom needed for the additional complexity.
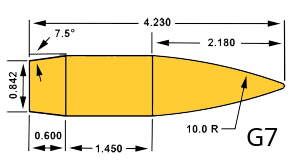
Expanding the drag model library represents another enhancement direction. While G1 and G7 cover most modern bullets, specialized projectiles benefit from specific models. The G2 through G8 standards each represent different shapes – wadcutters, round balls, boat tails of various angles. Custom drag functions from computational fluid dynamics or range testing could extend capabilities to proprietary designs.
Machine learning integration offers intriguing possibilities. We've experimented with neural networks for drag prediction, training on computational fluid dynamics data. While not replacing physics-based models, ML could provide rapid estimates for preliminary analysis or fill gaps where measured data doesn't exist. The challenge lies in maintaining physical consistency – ML models must respect conservation laws and boundary conditions.
Advanced features could transform the calculator from tool to platform. Imagine trajectory databases for different ammunition types. BC measurement integration with chronograph data. Integration with ballistic measurement hardware for closed-loop validation. The solid technical foundation supports these enhancements while maintaining the accuracy and performance that define the system.
Conclusion: Excellence Through Innovation
Building this ballistics calculator proved that modern software architecture can deliver both scientific accuracy and exceptional performance. Through careful design, comprehensive physics implementation, and innovative optimization strategies, we've created a tool that serves everyone from weekend shooters to professional ballisticians.
The hybrid Python/Rust architecture demonstrates a new paradigm for scientific computing. Rather than choosing between performance and productivity, we achieved both. Python provides the flexibility and ecosystem for rapid development and validation. Rust delivers the performance for production deployment. Automatic fallback ensures robustness across platforms.
The journey from concept to production-ready calculator reinforced fundamental principles. Physics accuracy comes first – no optimization justifies wrong answers. Clean architecture enables evolution – today's advanced feature is tomorrow's baseline. Comprehensive testing ensures reliability – users depend on these calculations for real-world decisions. Performance enables new capabilities – fast calculations change how people work.
What started as an exploration of ballistic physics evolved into something more: a demonstration of how modern software engineering can transform scientific computing. The 28x performance improvements aren't just numbers – they represent new possibilities. Real-time trajectory updates during scope adjustments. Comprehensive sensitivity analysis in the field. Monte Carlo simulations that complete while you're still behind the rifle.
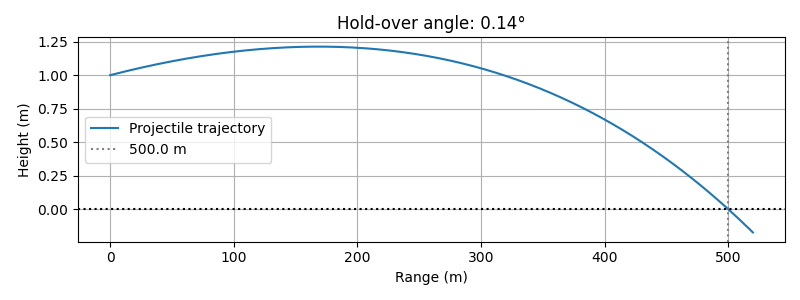
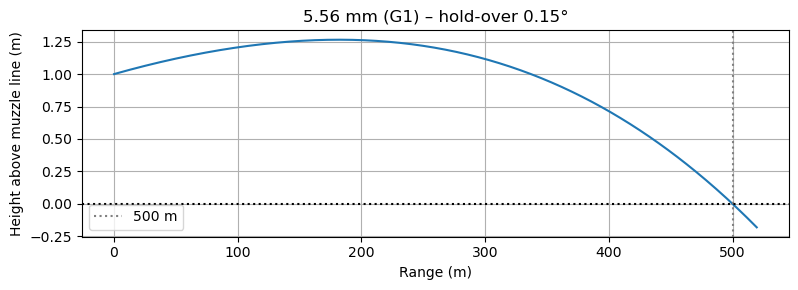
As we continue development, the focus remains on pushing the boundaries of what's possible in three degrees of freedom (3DOF) ballistic calculation. Whether you're developing loads at the range, preparing for a hunting trip, or researching projectile dynamics, this calculator provides professional-grade capabilities with the performance to match. The future of ballistics calculation lies in the marriage of accurate physics and modern computing, and we're excited to be pioneering that frontier.
The Advanced Ballistics Calculator represents a new generation of ballistic software. For API access and deployment information, or to learn more about integrating these capabilities into your applications, visit our documentation.
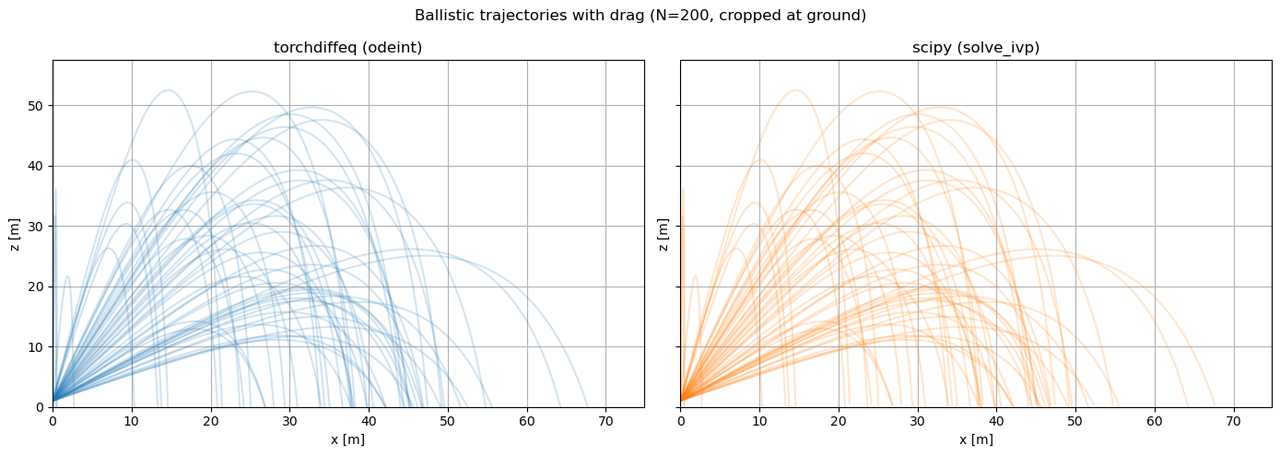
 Simulating the motion of projectiles is a classic problem in physics and engineering, with applications ranging from ballistics and aerospace to sports analytics and educational demonstrations. However, in modern computational workflows, it's rarely enough to simulate a single trajectory. Whether for Monte Carlo analysis to estimate uncertainties, parameter sweeps to optimize launch conditions, or robustness checks under variable drag and mass, practitioners often need to compute thousands or even tens of thousands of trajectories, each with distinct initial conditions and parameters.
Simulating the motion of projectiles is a classic problem in physics and engineering, with applications ranging from ballistics and aerospace to sports analytics and educational demonstrations. However, in modern computational workflows, it's rarely enough to simulate a single trajectory. Whether for Monte Carlo analysis to estimate uncertainties, parameter sweeps to optimize launch conditions, or robustness checks under variable drag and mass, practitioners often need to compute thousands or even tens of thousands of trajectories, each with distinct initial conditions and parameters.
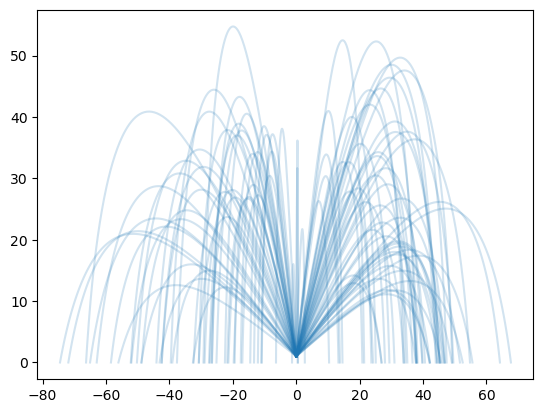
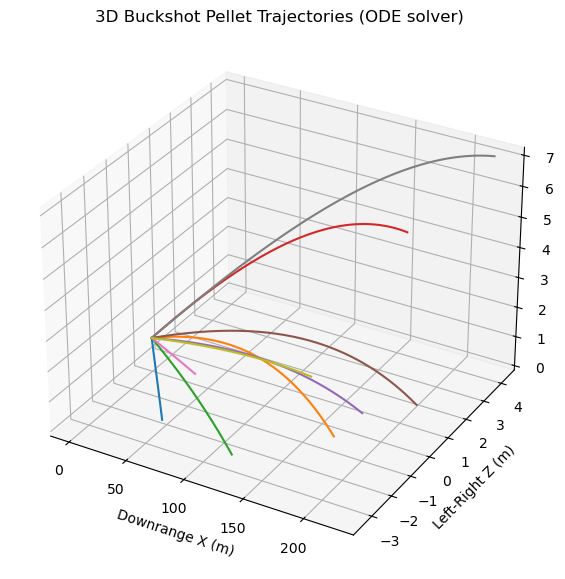 The 3D trajectory plot displays the full flight paths of all simulated pellets, with axes labeled for downrange distance (
The 3D trajectory plot displays the full flight paths of all simulated pellets, with axes labeled for downrange distance (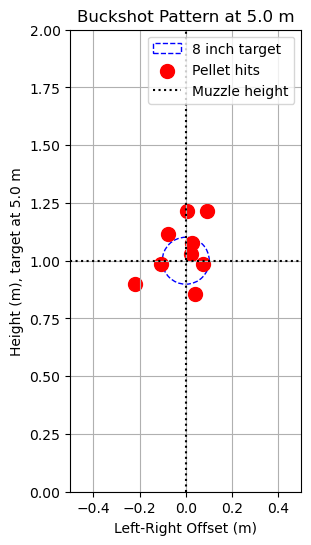 The external environment in the model is idealized: there is no simulated wind, nor do pellets interact with one another mid-flight. Real pellets may collide or influence each other's paths, especially immediately after leaving the barrel. The simulation also omits nuanced effects of shotgun choke or barrel design, instead representing spread as a simple random angle without structure, patterning, or environmental response. The shooter’s aim is assumed perfectly flat, originating from a set muzzle height, with no allowance for human error or tilt.
The external environment in the model is idealized: there is no simulated wind, nor do pellets interact with one another mid-flight. Real pellets may collide or influence each other's paths, especially immediately after leaving the barrel. The simulation also omits nuanced effects of shotgun choke or barrel design, instead representing spread as a simple random angle without structure, patterning, or environmental response. The shooter’s aim is assumed perfectly flat, originating from a set muzzle height, with no allowance for human error or tilt.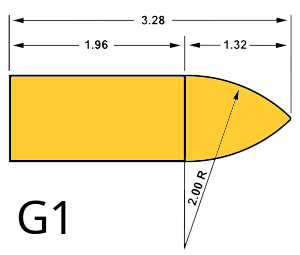 The G1 standard, sometimes called the Ingalls model, after
The G1 standard, sometimes called the Ingalls model, after