Shotguns are celebrated for their unique ability to launch a cluster of small projectiles—referred to as pellets—simultaneously, making them highly effective at short ranges in hunting, sport shooting, and defensive scenarios. The way these pellets separate and spread apart during flight creates the signature pattern seen on shotgun targets. While the general term “shot” applies to all such projectiles, specific pellet sizes exist, each with distinct ballistic properties. In this article, we will focus on modeling #00 buckshot, a popular choice for both self-defense and law enforcement applications due to its larger pellet size and stopping power.
By using Python, we’ll construct a simulation that predicts the paths and spread of #00 buckshot pellets after they leave the barrel. Drawing from principles of physics—like gravity and aerodynamic drag—and incorporating randomness to reflect real-world variation, our code will numerically solve each pellet’s flight path. This approach lets us visualize the resulting shot pattern at a chosen distance downrange and gain a deeper appreciation for how ballistic forces and initial conditions shape what happens when the trigger is pulled.
Understanding the Physics of Shotgun Pellets
When a shotgun is fired, each pellet exits the barrel at a significant velocity, starting a brief yet complex flight through the air. The physical forces acting on the pellets dictate their individual paths and, ultimately, the characteristic spread pattern observed at the target. To create an accurate simulation of this process, it’s important to understand the primary factors influencing pellet motion.
The most fundamental force is gravity. This constant downward pull, at approximately 9.81 meters per second squared, causes pellets to fall toward the earth as they travel forward. The effect of gravity is immediate: even with a rapid muzzle velocity, pellets begin to drop soon after leaving the barrel, and this drop becomes more noticeable over longer distances.
Another critical factor, particularly relevant for small and light projectiles such as #00 buckshot, is aerodynamic drag. As a pellet speeds through the air, it constantly encounters resistance from air molecules in its path. Drag not only oppose the pellet’s motion but also increases rapidly with speed—it is proportional to the square of the velocity. The magnitude of this force depends on properties such as the pellet’s cross-sectional area, mass, and shape (summarized by the drag coefficient). In this model, we assume all pellets are nearly spherical and share the same mass and size, using standard values for drag.
The interplay between gravity and aerodynamic drag controls how far each pellet travels and how much it slows before reaching the target. These forces are at the core of external ballistics, shaping how the tight column of pellets at the muzzle becomes a broad pattern by the time it arrives downrange. Understanding and accurately representing these effects is essential for any simulation that aims to realistically capture shotgun pellet motion.
Setting Up the Simulation
Before simulating shotgun pellet flight, the foundation of the model must be established through a series of physical parameters. These values are crucial—they dictate everything from the amount of drag experienced by a pellet to the degree of possible spread observed on a target.
First, the code defines characteristics of a single #00 buckshot pellet. The pellet diameter (d) is set to 0.0084 meters, giving a radius (r) of half that value. The cross-sectional area (A) is calculated as π times the radius squared. This area directly impacts how much air resistance the pellet experiences—the larger the cross-section, the more drag slows it down. The mass (m) is set to 0.00351 kilograms, representing the weight of an individual #00 pellet in a standard shotgun load.
Next, the code specifies values needed for the calculation of aerodynamic drag. The drag coefficient (Cd) is set to 0.47, a typical value for a sphere moving through air. Air density (rho) is specified as 1.225 kilograms per cubic meter, which is a standard value at sea level under average conditions. Gravity (g) is established as 9.81 meters per second squared.
The number of pellets to simulate is set with num_pellets; here, nine pellets are used, reflecting a common #00 buckshot shell configuration. The v0 parameter sets the initial (muzzle) velocity for each pellet, at 370 meters per second—a realistic value for modern 12-gauge loads. To add realism, slight random variation in velocity is included using v_sigma, which allows muzzle velocity to be sampled from a normal distribution for each pellet. This captures the real-world variability inherent in a shotgun shot.
To model the spread of pellets as they leave the barrel, the code uses spread_std_deg and spread_max_deg. These parameters define the standard deviation and maximum value for the random angular deviation of each pellet in both horizontal and vertical directions. This gives each pellet a unique initial direction, simulating the inherent randomness and choke effect seen in actual shotgun blasts.
Initial position coordinates (x0, y0, z0) establish where the pellets start—here, at the muzzle, with the barrel one meter off the ground. The pattern_distance defines how far away the “target” is placed, setting the plane where pellet impacts are measured. Finally, max_time sets a hard cap on the simulated flight duration, ensuring computations finish even if a pellet never hits the ground or target.
By specifying all these parameters before running the simulation, the code grounds its calculations in real-world physical properties, establishing a robust and realistic baseline for the ODE-based modeling that follows.
The ODE Model
At the heart of the simulation is a mathematical model that describes each pellet’s motion using an ordinary differential equation (ODE). The state of a pellet in flight is captured by six variables: its position in three dimensions (x, y, z) and its velocity in each direction (vx, vy, vz). As the pellet travels, both gravity and aerodynamic drag act on it, continually altering its velocity and trajectory.
Gravity is straightforward in the model—a constant downward acceleration, reducing the y-component (height) of the pellet’s velocity over time. The trickier part is aerodynamic drag, which opposes the pellet’s motion and depends on both its speed and orientation. In this simulation, drag is modeled using the standard quadratic law, which states that the decelerating force is proportional to the square of the velocity. Mathematically, the drag acceleration in each direction is calculated as:
dv/dt = -k * v * v_dir
where k bundles together the effects of drag coefficient, air density, area, and mass, v is the current speed, and v_dir is a velocity component (vx, vy, or vz).
Within the pellet_ode function, the code computes the combined velocity from its three components and then applies this drag to each directional velocity. Gravity appears as a constant subtraction from the vertical (vy) acceleration. The ODE function returns the derivatives of all six state variables, which are then numerically integrated over time using Scipy’s solve_ivp routine.
By combining these physics-based rules, the ODE produces realistic pellet flight paths, showing how each is steadily slowed by drag and pulled downward by gravity on its journey from muzzle to target.
Modeling Pellet Spread: Incorporating Randomness
A defining feature of shotgun use is the spread of pellets as they exit the barrel and travel toward the target. While the physics of flight create predictable paths, the divergence of each pellet from the bore axis is largely random, influenced by manufacturing tolerances, barrel choke, and small perturbations at ignition. To replicate this in simulation, the code incorporates controlled randomness into the initial direction and velocity of each pellet.
For every simulated pellet, two angles are generated: one for vertical (up-down) deviation and one for horizontal (left-right) deviation. These angles are drawn from a normal (Gaussian) distribution centered at zero, reflecting the natural scatter expected from a well-maintained shotgun. Standard deviation and maximum values—set by spread_std_deg and spread_max_deg—control the tightness and outer limits of this spread. This ensures realistic variation while preventing extreme outliers not seen in practice.
Muzzle velocity is also subject to small random variation. While the manufacturer’s rating might place velocity at 370 meters per second, factors like ammunition inconsistencies and environmental conditions can introduce fluctuations. By sampling the initial velocity for each pellet from a normal distribution (with mean v0 and standard deviation v_sigma), the simulator reproduces this subtle randomness.
To determine starting velocities in three dimensions (vx, vy, vz), the code applies trigonometric calculations based on the sampled initial angles and speed, ensuring that each pellet’s departure vector deviates uniquely from the barrel’s axis. The result is a spread pattern that closely mirrors those seen in field tests—a dense central cluster with some pellets landing closer to the edge.
By weaving calculated randomness into the simulation’s initial conditions, the code not only matches the unpredictable nature of real-world shot patterns, but also creates meaningful output for analyzing shotgun effectiveness and pattern density at various distances.
ODE Integration with Boundary Events
Simulating the trajectory of each pellet requires numerically solving the equations of motion over time. This is accomplished by passing the ODE model to SciPy’s solve_ivp function, which integrates the system from the pellet’s moment of exit until it either hits the ground, the target plane, or a maximum time is reached. To handle these criteria efficiently, the code employs two “event” functions that monitor for specific conditions during integration.
The first event, ground_event, is triggered when a pellet’s vertical position (y) reaches zero, corresponding to ground impact. This event is marked as terminal in the integration, so once triggered, the ODE solver halts further calculation for that pellet—ensuring we don’t simulate motion beneath the earth.
The second event, pattern_event, fires when the pellet’s downrange distance (x) equals the designated pattern distance. This captures the precise moment a pellet crosses the plane of interest, such as a target board at 5 meters. Unlike ground_event, this event is not terminal, allowing the solver to keep tracking the pellet in case it flies beyond the target distance before landing.
By combining these event-driven stops with dense output (for smooth interpolation) and a small integration step size, the code accurately and efficiently identifies either the ground impact or the target crossing for each pellet. This strategy ensures that every significant outcome in the flight—whether a hit or a miss—is reliably captured in the simulation.
import numpy as np from scipy.integrate import solve_ivp import matplotlib.pyplot as plt # Physical constants d = 0.0084 # m r = d / 2 A = np.pi * r**2 # m^2 m = 0.00351 # kg Cd = 0.47 rho = 1.225 # kg/m^3 g = 9.81 # m/s^2 num_pellets = 9 v0 = 370 # muzzle velocity m/s v_sigma = 10 spread_std_deg = 1.2 spread_max_deg = 2.5 x0, y0, z0 = 0., 1.0, 0. pattern_distance = 5.0 # m max_time = 1.0 def pellet_ode(t, y): vx, vy, vz = y[3:6] v = np.sqrt(vx**2 + vy**2 + vz**2) k = 0.5 * Cd * rho * A / m dxdt = vx dydt = vy dzdt = vz dvxdt = -k * v * vx dvydt = -k * v * vy - g dvzdt = -k * v * vz return [dxdt, dydt, dzdt, dvxdt, dvydt, dvzdt] pattern_z = [] pattern_y = [] trajectories = [] for i in range(num_pellets): # Randomize initial direction for spread theta_h = np.random.normal(0, np.radians(spread_std_deg)) theta_h = np.clip(theta_h, -np.radians(spread_max_deg), np.radians(spread_max_deg)) theta_v = np.random.normal(0, np.radians(spread_std_deg)) theta_v = np.clip(theta_v, -np.radians(spread_max_deg), np.radians(spread_max_deg)) v0p = np.random.normal(v0, v_sigma) # Forward is X axis. Up is Y axis. Left-right is Z axis vx0 = v0p * np.cos(theta_v) * np.cos(theta_h) vy0 = v0p * np.sin(theta_v) vz0 = v0p * np.cos(theta_v) * np.sin(theta_h) ic = [x0, y0, z0, vx0, vy0, vz0] def ground_event(t, y): # y[1] is height return y[1] ground_event.terminal = True ground_event.direction = -1 def pattern_event(t, y): # y[0] is x return y[0] - pattern_distance pattern_event.terminal = False pattern_event.direction = 1 sol = solve_ivp( pellet_ode, [0, max_time], ic, events=[ground_event, pattern_event], dense_output=True, max_step=0.01 ) # Find the stopping time: whichever is first, ground or simulation end if sol.t_events[0].size > 0: t_end = sol.t_events[0][0] else: t_end = sol.t[-1] t_plot = np.linspace(0, t_end, 200) trajectories.append(sol.sol(t_plot)) # Interpolate to pattern_distance for hit pattern x = sol.y[0] if np.any(x >= pattern_distance): idx = np.argmax(x >= pattern_distance) if idx > 0: # avoid index out of bounds if already starting beyond pattern_distance frac = (pattern_distance - x[idx-1]) / (x[idx] - x[idx-1]) zhit = sol.y[2][idx-1] + frac * (sol.y[2][idx] - sol.y[2][idx-1]) yhit = sol.y[1][idx-1] + frac * (sol.y[1][idx] - sol.y[1][idx-1]) if yhit > 0: pattern_z.append(zhit) pattern_y.append(yhit) # --- Plot 3D trajectories --- fig = plt.figure(figsize=(12,7)) ax = fig.add_subplot(111, projection='3d') for traj in trajectories: x, y, z, vx, vy, vz = traj ax.plot(x, z, y) ax.set_xlabel('Downrange X (m)') ax.set_ylabel('Left-Right Z (m)') ax.set_zlabel('Height Y (m)') ax.set_title('3D Buckshot Pellet Trajectories (ODE solver)') plt.show() # --- Plot pattern on 25m target plane --- plt.figure(figsize=(8,6)) circle = plt.Circle((0,1), 0.2032/2, color='b', fill=False, linestyle='--', label='8 inch target') plt.gca().add_patch(circle) plt.scatter(pattern_z, pattern_y, c='r', s=100, marker='o', label='Pellet hits') plt.xlabel('Left-Right Offset (m)') plt.ylabel(f'Height (m), target at {pattern_distance} m') plt.title(f'Buckshot Pattern at {pattern_distance} m') plt.axhline(1, color='k', ls=':', label='Muzzle height') plt.axvline(0, color='k', ls=':') plt.ylim(0, 2) plt.xlim(-0.5, 0.5) plt.legend() plt.grid(True) plt.gca().set_aspect('equal', adjustable='box') plt.show()
Recording and Visualizing Pellet Impacts
Once a pellet’s trajectory has been simulated, it is important to determine exactly where it would strike the target plane placed at the specified downrange distance. Because the pellet’s position is updated in discrete time steps, it rarely lands exactly at the pattern_distance. Therefore, the code detects when the pellet’s simulated x-position first passes this distance. At this point, a linear interpolation is performed between the two positions bracketing the target plane, calculating the precise y (height) and z (left-right) coordinates where the pellet would intersect the pattern distance. This ensures consistent and accurate hit placement regardless of integration step size.
The resulting values for each pellet are appended to the pattern_y and pattern_z lists. These lists collectively represent the full group of pellet impact points at the target plane and can be conveniently visualized or analyzed further.
By recording these interpolated impact points, the simulation offers direct insight into the spatial distribution of pellets on the target. This data allows shooters and engineers to assess key real-world characteristics such as pattern density, evenness, and the likelihood of hitting a given area. In visualization, these points paint a clear picture of spread and clustering, helping to understand both shotgun effectiveness and pellet behavior under the influence of drag and gravity.
Visualization: Plotting Trajectories and Impact Patterns
Visualizing the results of the simulation offers both an intuitive understanding of pellet motion and practical insight into shotgun performance. The code provides two types of plots: a three-dimensional trajectory plot and a two-dimensional pattern plot on the target plane.
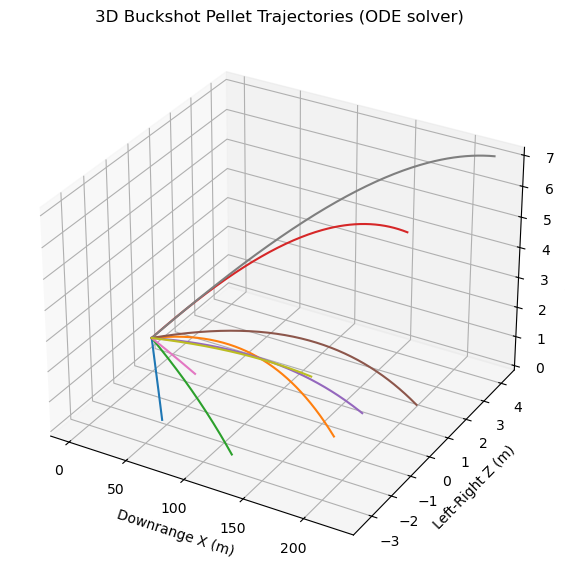The 3D trajectory plot displays the full flight paths of all simulated pellets, with axes labeled for downrange distance (x), left-right offset (z), and vertical height (y). Each pellet's arc is traced from muzzle exit to endpoint, revealing not just forward travel and fall due to gravity, but also the sideways spread caused by angular deviation and drag. This plot gives a comprehensive, real-time sense of how pellets diverge and lose height, much like visualizing the flight of shot in slow motion. It can highlight trends such as gradual drop-offs, the effect of random spread angles, and which pellets remain above the ground longest.
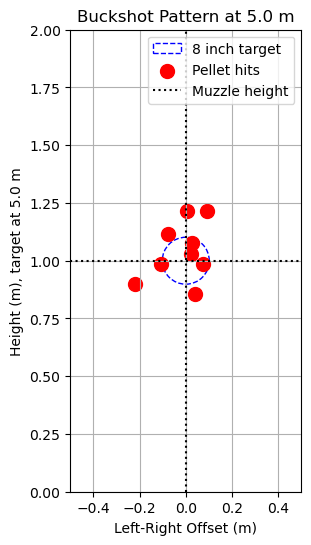
The pattern plane plot focuses on practical outcomes—the locations where pellets would strike a target at a given distance (e.g., 5 meters downrange). An 8-inch circle is superimposed to represent a common target size, providing context for real-world shooting scenarios. Each simulated impact point is marked, showing the actual distribution and clustering of pellets. Reference lines denote the muzzle height (horizontal) and the barrel center (vertical), helping to orient the viewer and relate simulated results to how a shooter would aim.
Together, these visuals bridge the gap between abstract trajectory calculations and real shooting experience. The 3D plot helps explore external ballistics, while the pattern plot reflects what a shooter would see on a paper target at the range—key information for understanding spread, pattern density, and shotgun effectiveness.
Assumptions & Limitations of the Model
While this simulation offers a physically grounded view of #00 buckshot spread, several simplifying assumptions shape its results. The code treats all pellets as perfectly spherical, identical in size and mass, and does not account for pellet deformation or fracturing—both of which can occur during firing or impact. Air properties are held constant, with fixed density and drag coefficient values; in reality, both can change due to weather, altitude, and even fluctuations in pellet speed.
The external environment in the model is idealized: there is no simulated wind, nor do pellets interact with one another mid-flight. Real pellets may collide or influence each other's paths, especially immediately after leaving the barrel. The simulation also omits nuanced effects of shotgun choke or barrel design, instead representing spread as a simple random angle without structure, patterning, or environmental response. The shooter’s aim is assumed perfectly flat, originating from a set muzzle height, with no allowance for human error or tilt.
These simplifications mean that actual shotgun patterns may differ in meaningful ways. Real-world patterns can display uneven density, elliptical shapes from chokes, or wind-induced drift—all absent from this model. Furthermore, pellet deformation can lead to less predictable spread, and varying air conditions or shooter input can add additional variability. Nevertheless, the simulation provides a valuable baseline for understanding the primary forces and expected outcomes, even if it cannot capture every subtlety from live fire.
Possible Improvements and Extensions
This simulation, while useful for visualizing basic pellet dynamics, could be made more realistic by addressing some of its idealizations. Incorporating wind modeling would add lateral drift, making the simulation more applicable to outdoor shooting scenarios. Simulating non-spherical or deformed pellets—accounting for variations in shape, mass, or surface—could change each pellet’s drag and produce more irregular spread patterns. Introducing explicit choke effects would allow for non-uniform or elliptical spreads that better match the output from different shotgun barrels and constrictions.
Environmental factors like altitude and temperature could be included to adjust air density and drag coefficient dynamically, reflecting their real influence on ballistics. Finally, modeling shooter-related factors such as sight alignment, aim variation, or recoil-induced muzzle movement would add further variability. Collectively, these enhancements would move the simulation closer to the unpredictable reality of shotgun use, providing even greater value for shooters, ballistics researchers, and enthusiasts alike.
Conclusion
Physically-accurate simulations of shotgun pellet spread offer valuable lessons for both programmers and shooting enthusiasts. By translating real-world ballistics into code, we gain a deeper understanding of the factors that shape shot patterns and how subtle changes in variables can influence outcomes. Python, paired with SciPy’s ODE solvers, proves to be an accessible and powerful toolkit for exploring these complex systems. Whether used for educational insight, hobby experimentation, or designing safer and more effective ammunition, this approach opens the door to further exploration. Readers are encouraged to adapt, extend, or refine the code to match their own interests and scenarios.