Interior ballistics is the study of processes that occur inside a firearm from the moment the primer ignites the propellant until the projectile exits the muzzle. This field is crucial for understanding and optimizing firearm performance, ammunition design, and firearm safety. At its core, interior ballistics involves the interaction between expanding gases generated by burning propellant and the resulting acceleration of the projectile through the barrel.
When a cartridge is fired, the primer ignites the propellant (gunpowder), rapidly converting it into high-pressure gases. This sudden gas expansion generates immense pressure within the firearm’s chamber. The pressure exerted on the projectile’s base forces it to accelerate forward along the barrel. The magnitude and duration of this pressure directly influence the projectile's muzzle velocity, trajectory, and ultimately, its performance and effectiveness.
Several factors profoundly influence interior ballistic performance. Propellant type significantly affects how rapidly gases expand and the rate at which pressure peaks and dissipates. Propellant mass determines the amount of energy available for projectile acceleration, while barrel length directly affects the time available for acceleration, thus impacting muzzle velocity. Bore area—the cross-sectional area of the barrel—also determines how effectively pressure translates into forward projectile motion.
From a theoretical standpoint, interior ballistics heavily relies on principles from thermodynamics and gas dynamics. The ideal gas law, describing the relationship between pressure, volume, and temperature, provides a foundational model for predicting pressure changes within the firearm barrel. Additionally, understanding propellant burn rates—which depend on pressure and grain geometry—is crucial for accurately modeling the internal combustion process.
By combining these theoretical principles with computational modeling techniques, precise predictions and optimizations become possible. Accurately simulating interior ballistics allows for safer firearm designs, enhanced projectile performance, and the development of more efficient ammunition.
The simulation model presented here specifically addresses the 5.56 NATO cartridge, widely used in military and civilian firearms. Key specifications for this cartridge include a bullet mass of approximately 4 grams, a typical barrel length of 20 inches (0.508 meters), and a bore diameter of approximately 5.56 millimeters. These physical and geometric parameters are foundational for accurate modeling.
Our simulation employs an Ordinary Differential Equation (ODE) approach to numerically model the dynamic behavior of pressure and projectile acceleration within the firearm barrel. This method involves setting up differential equations that represent mass, momentum, and energy balances within the system. We solve these equations using SciPy’s numerical solver, solve_ivp, specifically employing the Runge-Kutta method for enhanced accuracy and stability.
Several simplifying assumptions have been made in our model to balance complexity and computational efficiency. Primarily, the gases are assumed to behave ideally, following the ideal gas law without considering non-ideal effects such as frictional losses or heat transfer to the barrel walls. Additionally, we assume uniform burn rate parameters, which simplifies the propellant combustion dynamics. While these simplifications allow for faster computation and clearer insights into the primary ballistic behavior, they inherently limit the model's precision under extreme or highly variable conditions. Nevertheless, the chosen approach provides a robust and insightful basis for further analysis and optimization.
import numpy as np import matplotlib.pyplot as plt from scipy.integrate import solve_ivp # Parameters for 5.56 NATO interior ballistics m_bullet = 0.004 # kg m_propellant = 0.0017 # kg A_bore = 2.41e-5 # m^2 (5.56 mm diameter) barrel_length = 0.508 # m (20 inches) V_chamber_initial = 0.7e-5 # m^3 (further reduced chamber volume) rho_propellant = 1600 # kg/m^3 a, n = 5.0e-10, 2.9 # further adjusted for correct pressure spike E_propellant = 5.5e6 # J/kg (increased energy density) gamma = 1.25 # ODE System def interior_ballistics(t, y): """ System of ODEs describing the interior ballistics of a firearm. Parameters: t (float): Time y (list): State variables [x, v, m_g, U] Returns: list: Derivatives of state variables [dx_dt, dv_dt, dm_g_dt, dU_dt] """ x, v, m_g, U = y V = V_chamber_initial + A_bore * x p = (gamma - 1) * U / V burn_rate = a * p ** n A_burn = rho_propellant * A_bore * 0.065 # significantly adjusted dm_g_dt = rho_propellant * A_burn * burn_rate if m_g < m_propellant else 0 dQ_burn_dt = E_propellant * dm_g_dt dV_dt = A_bore * v dU_dt = dQ_burn_dt - p * dV_dt dv_dt = (A_bore * p) / m_bullet if x < barrel_length else 0 dx_dt = v if x < barrel_length else 0 return [dx_dt, dv_dt, dm_g_dt, dU_dt] # Initial Conditions y0 = [0, 0, 0, 1e5 * V_chamber_initial / (gamma - 1)] t_span = (0, 0.0015) # simulate until projectile exits barrel solution = solve_ivp(interior_ballistics, t_span, y0, method='RK45', max_step=1e-8) # Results extraction time = solution.t * 1e3 # convert time to milliseconds x, v, m_g, U = solution.y # Calculate pressure V = V_chamber_initial + A_bore * x pressure = (gamma - 1) * U / V / 1e6 # convert pressure to MPa # Print final velocity final_velocity = v[-1] print(f"Final velocity of the bullet: {final_velocity:.2f} m/s") # Graphing the corrected pressure-time and velocity-time curves plt.figure(figsize=(12, 6)) plt.subplot(1, 2, 1) plt.plot(time, pressure, label='Chamber Pressure') plt.xlabel('Time (ms)') plt.ylabel('Pressure (MPa)') plt.title('Pressure-Time Curve') plt.grid(True) plt.legend() plt.subplot(1, 2, 2) plt.plot(time, v, label='Bullet Velocity') plt.xlabel('Time (ms)') plt.ylabel('Velocity (m/s)') plt.title('Velocity-Time Curve') plt.grid(True) plt.legend() plt.tight_layout() plt.show()
The Python code for our model uses carefully selected physical parameters to achieve realistic results. Key parameters include the bullet mass (m_bullet), propellant mass (m_propellant), bore area (A_bore), initial chamber volume (V_chamber_initial), propellant density (rho_propellant), specific heat ratio (gamma), and propellant burn parameters (a, n, E_propellant). Accurate parameter selection ensures the fidelity of the simulation results, as small changes significantly impact predictions of bullet velocity and chamber pressure.
The simulation revolves around an ODE system representing the dynamics within the barrel. The state variables include bullet position (x), bullet velocity (v), mass of burnt propellant (m_g), and internal gas energy (U). Bullet position and velocity are critical for tracking projectile acceleration and determining when the projectile exits the barrel. Mass of burnt propellant tracks combustion progression, directly influencing gas generation and pressure. Internal gas energy accounts for the thermodynamics of gas expansion and work performed on the projectile.
The ODE system equations describe propellant combustion rates, chamber pressure, and projectile acceleration. Propellant burn rate is pressure-dependent, modeled using an empirical power-law relationship. Chamber pressure is derived from the internal energy and chamber volume, expanding as the projectile moves forward. Projectile acceleration is calculated based on pressure force applied over the bore area. Conditional checks ensure realistic behavior, stopping propellant combustion once all propellant is consumed and halting projectile acceleration once it exits the barrel, thus maintaining physical accuracy.
Initial conditions (y0) represent the physical state at ignition: zero initial bullet velocity and position, no burnt propellant, and a small initial gas energy corresponding to ambient conditions. The numerical solver parameters, including the Runge-Kutta (RK45) method and a small maximum step size (max_step), were chosen to balance computational efficiency with accuracy. These settings provide stable and accurate solutions for the rapid dynamics typical of interior ballistics scenarios.
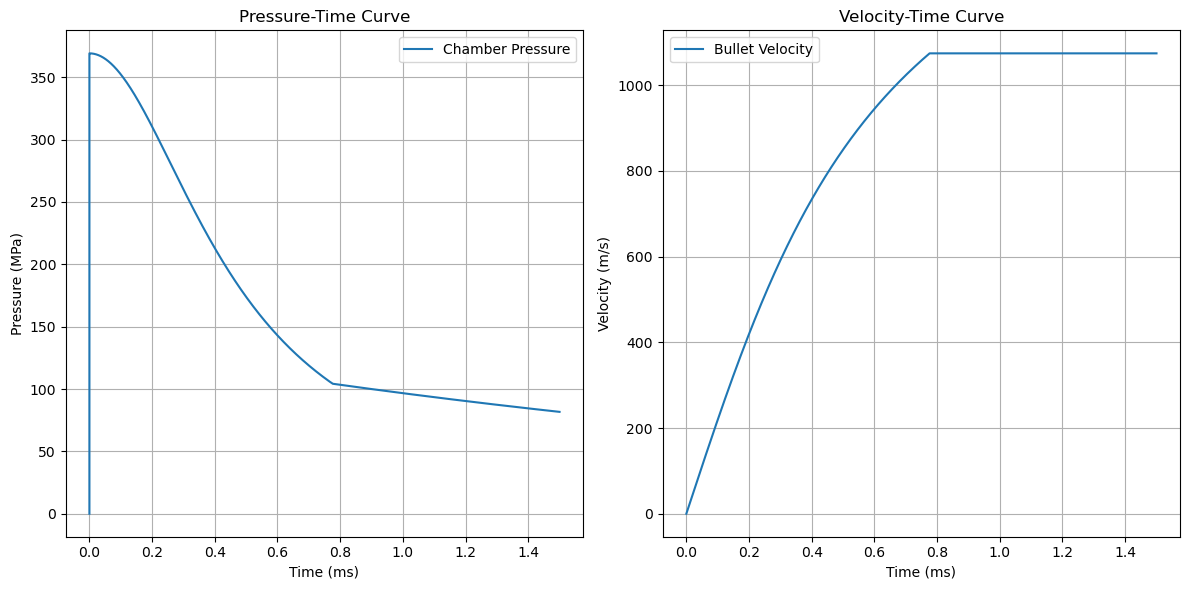
Analyzing the simulation results provides critical insights into ballistic performance. Typical results include detailed bullet velocity and chamber pressure profiles, showing rapid acceleration and pressure dynamics throughout the bullet’s travel in the barrel. Identifying peak pressure is particularly significant as it indicates the maximum stress experienced by firearm components and influences safety and design criteria.
Pressure-time graphs are vital tools for visualization, clearly illustrating how pressure sharply rises to its peak early in the firing event and then rapidly declines as gases expand and the bullet accelerates down the barrel. Comparing these simulation outputs with empirical or published ballistic data confirms the validity and accuracy of the model, ensuring its practical applicability for firearm and ammunition design and analysis.
Validating the accuracy of this model involves addressing potential concerns such as the realism of the chosen simulation timescale. The duration of 1–2 milliseconds is realistic based on typical bullet velocities and barrel lengths for the 5.56 NATO cartridge. Real-world ballistic testing data confirms the general accuracy of the predicted pressure peaks and velocity profiles. Conducting sensitivity analyses—varying parameters such as burn rates, propellant mass, and barrel length—helps understand their impacts on ballistic outcomes. For further validation and accuracy improvement, readers are encouraged to use actual ballistic chronograph data and to explore more complex modeling, including detailed gas dynamics, heat transfer, and friction effects within the barrel.
Practical applications of interior ballistic simulations extend broadly to firearm and ammunition design optimization. Manufacturers, researchers, military organizations, and law enforcement agencies rely on such models to improve cartridge efficiency, optimize barrel designs, and enhance overall firearm safety and effectiveness. Additionally, forensic investigations utilize similar modeling techniques to reconstruct firearm-related incidents, helping to provide insights into ballistic events. Future extensions to this simulation model could include integration with external ballistics for trajectory analysis post-barrel exit and incorporating advanced thermodynamic refinements like real gas equations, heat transfer effects, and friction modeling for enhanced predictive accuracy.