Introduction
Ballistics simulation plays a critical role across various sectors, from defense applications to sports shooting, hunting, and law enforcement training, by enabling precise predictions of projectile trajectories, velocities, and impacts. At the core of ballistics, the branch known as interior ballistics focuses on projectile behavior from ignition until the bullet exits the barrel. Understanding and accurately modeling this phase is essential, as even minor deviations can lead to significant errors downrange, affecting performance, safety, reliability, mission outcomes, and competitive advantages.
Accurate ballistic predictions ensure optimal firearm and ammunition designs, enhance operator safety, and improve resource efficiency. Traditional modeling techniques typically involve solving ordinary differential equations (ODEs), providing a robust framework grounded in physics. However, these models are computationally demanding and highly sensitive to parameter changes. Advances in firearm and projectile technology necessitate models that manage complexity without sacrificing accuracy, prompting exploration into methods that combine traditional physics-based approaches with modern computational techniques.
The Role of Machine Learning in Ballistics Simulation
Machine learning methods have emerged as potent tools for enhancing traditional simulations, delivering increased efficiency, flexibility, and adaptability to varying parameters and environmental conditions. By training machine learning models on extensive simulated data, ballistic predictions can rapidly adapt to diverse conditions without repeatedly solving complex equations, significantly reducing computational time and resource requirements. machine learning algorithms excel at recognizing patterns within large datasets, thereby enhancing predictive performance and robustness.
Furthermore, machine learning techniques can be employed to identify key factors influencing ballistic performance, allowing for targeted optimization of firearm and ammunition designs. For instance, machine learning algorithms can be used to analyze the impact of propellant characteristics, barrel geometry, and environmental conditions on bullet velocity and accuracy. By leveraging machine learning methods, researchers and engineers can efficiently explore the vast design space of ballistic systems, accelerating the development of high-performance firearms and ammunition.
Hybrid Approach: Combining Physics-Based Simulations with Machine Learning
This blog explores an integrated approach combining detailed physical modeling through numerical ODE simulations and advanced machine learning techniques to predict bullet velocity accurately. We will discuss theoretical foundations, Python-based simulation techniques, Random Forest regression implementation, and demonstrate how this hybrid method enhances prediction accuracy and computational efficiency. This innovative approach not only advances interior ballistics modeling but also expands possibilities for future applications in simulation-driven design and real-time ballistic solutions.
The hybrid approach leverages the strengths of both physics-based simulations and machine learning techniques, combining the accuracy and interpretability of physical models with the efficiency and adaptability of machine learning algorithms. By integrating these two approaches, the hybrid method can capture complex interactions and nonlinear relationships within ballistic systems, leading to more accurate and robust predictions. Furthermore, the hybrid approach enables the efficient exploration of design spaces, facilitating the optimization of firearm and ammunition designs.
Theoretical Foundations and Simulation Techniques
Interior ballistics studies projectile behavior from propellant ignition to the projectile exiting the firearm barrel. This phase critically determines the projectile’s initial velocity and trajectory, significantly impacting accuracy and effectiveness. Proper modeling and understanding of interior ballistics are vital for optimizing firearm designs, ammunition performance, operational reliability, and ensuring safety.
Key interior ballistic variables include:
- Pressure: Pressure within the barrel directly accelerates the projectile; greater pressures typically yield higher velocities but necessitate stringent safety measures.
- Velocity: The projectile's velocity is a critical factor in determining its trajectory and impact.
- Propellant Mass: Propellant mass dictates available energy, significantly influencing pressure dynamics.
- Bore Area: The bore area—the barrel’s cross-sectional area—affects pressure distribution and the efficiency of energy transfer from propellant to projectile.
The governing equations of interior ballistics rest on energy conservation principles and propellant mass burn rate dynamics. Energy conservation equations describe how chemical energy from propellant combustion transforms into kinetic energy of the projectile and thermal energy within the barrel. Mass burn rate equations quantify the consumption rate of propellant, influencing pressure development within the barrel. Accurate numerical solutions to these equations ensure reliable predictions, optimize ammunition designs, and enhance firearm safety.
To accurately model interior ballistics, numerical methods such as the Runge-Kutta method or finite difference methods are employed to solve the governing equations. These numerical methods provide approximate solutions to the ODEs, enabling the simulation of complex ballistic phenomena. The choice of numerical method depends on factors such as accuracy, computational efficiency, and stability. In this blog, we utilize the solve_ivp function from scipy.integrate to solve the interior ballistics ODE system.
Numerical Modeling and Python Implementation
The provided Python code utilizes the solve_ivp function from scipy.integrate to solve the interior ballistics ODE system. The code defines the ODE system, generates data for machine learning training, trains a Random Forest regressor, and evaluates its performance.
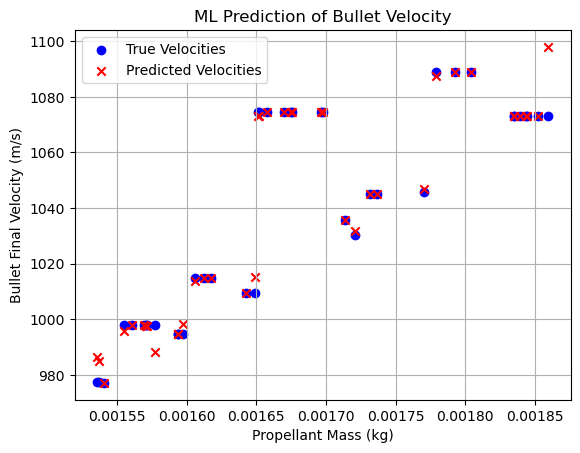
import numpy as np import matplotlib.pyplot as plt from scipy.integrate import solve_ivp from sklearn.ensemble import RandomForestRegressor from sklearn.model_selection import train_test_split from sklearn.metrics import mean_squared_error # Original parameters m_bullet = 0.004 m_propellant = 0.0017 A_bore = 2.41e-5 barrel_length = 0.508 V_chamber_initial = 0.7e-5 rho_propellant = 1600 a, n = 5.0e-10, 2.9 E_propellant = 5.5e6 gamma = 1.25 # Interior ballistics ODE system def interior_ballistics(t, y, propellant_mass): x, v, m_g, U = y V = V_chamber_initial + A_bore * x p = (gamma - 1) * U / V burn_rate = a * p**n A_burn = rho_propellant * A_bore * 0.065 dm_g_dt = rho_propellant * A_burn * burn_rate if m_g < propellant_mass else 0 dQ_burn_dt = E_propellant * dm_g_dt dV_dt = A_bore * v dU_dt = dQ_burn_dt - p * dV_dt dv_dt = (A_bore * p) / m_bullet if x < barrel_length else 0 dx_dt = v if x < barrel_length else 0 return [dx_dt, dv_dt, dm_g_dt, dU_dt] # Generate data for machine learning training n_samples = 200 X, y = [], [] np.random.seed(42) for _ in range(n_samples): # Vary propellant mass slightly for training data propellant_mass = m_propellant * np.random.uniform(0.9, 1.1) y0 = [0, 0, 0, 1e5 * V_chamber_initial / (gamma - 1)] solution = solve_ivp( interior_ballistics, [0, 0.0015], y0, args=(propellant_mass,), method='RK45', max_step=1e-8 ) final_velocity = solution.y[1, -1] X.append([propellant_mass]) y.append(final_velocity) X = np.array(X) y = np.array(y) # Split data X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2) #,random_state=42) # machine learning model training model = RandomForestRegressor(n_estimators=100) #,random_state=42) model.fit(X_train, y_train) # Prediction and evaluation y_pred = model.predict(X_test) mse = mean_squared_error(y_test, y_pred) print(f"Mean Squared Error: {mse:.4f}") y_train_pred = model.predict(X_train) train_mse = mean_squared_error(y_train, y_train_pred) print(f"Train MSE: {train_mse:.4f}") # Visualization plt.scatter(X_test, y_test, color='blue', label='True Velocities') plt.scatter(X_test, y_pred, color='red', marker='x', label='Predicted Velocities') plt.xlabel('Propellant Mass (kg)') plt.ylabel('Bullet Final Velocity (m/s)') plt.title('ML Prediction of Bullet Velocity') plt.grid(True) plt.legend() plt.show()
Practical Applications and Implications
The integration of physics-based simulations with machine learning has demonstrated substantial benefits in accurately predicting bullet velocities. This hybrid modeling approach effectively combines the rigorous scientific accuracy of physical simulations with the computational efficiency and adaptability of machine learning methods. By employing numerical ODE simulations and Random Forest regression, the approach achieved strong predictive accuracy, evidenced by low MSE values on both training and testing datasets, and confirmed through visualization.
The practical implications of this hybrid approach include:
- Reduced Computational Resources: The hybrid approach significantly reduces the computational resources required for ballistic simulations.
- Faster Predictions: The model provides faster predictions, enabling rapid evaluation of different scenarios and design parameters.
- Improved Adaptability: The approach can adapt to variations in propellant characteristics and environmental conditions, enhancing its utility in real-world applications.
Advantages of Hybrid Approach
The hybrid approach offers several advantages over traditional methods:
- Improved Accuracy: The combination of physics-based simulations and machine learning techniques leads to more accurate predictions.
- Increased Efficiency: The approach reduces computational time and resource requirements.
- Flexibility: The model can be easily adapted to different propellant characteristics and environmental conditions.
Limitations and Future Directions
While the hybrid approach has shown significant potential, there are limitations and future directions to consider:
- Data Quality: The accuracy of the machine learning model depends on the quality and quantity of the training data.
- Complexity: The approach requires a good understanding of the underlying physics and machine learning techniques.
- Scalability: The approach can be computationally intensive for large datasets and complex simulations.
Future directions include:
- Integrating Additional Parameters: Incorporating additional parameters, such as varying bullet weights, barrel lengths, and environmental conditions, can improve model robustness and predictive accuracy.
- Employing More Complex machine learning Models: Utilizing more complex machine learning models, such as neural networks or gradient boosting algorithms, could further enhance performance.
- Real-World Applications: The approach can be applied to real-world scenarios, such as designing new firearms and ammunition, optimizing existing designs, and predicting ballistic performance under various conditions.
Additionally, future research can focus on:
- Uncertainty Quantification: Developing methods to quantify uncertainty in the predictions, enabling more informed decision-making.
- Sensitivity Analysis: Conducting sensitivity analysis to understand the impact of input parameters on the predictions.
- Multi-Physics Simulations: Integrating multiple physics, such as thermodynamics and fluid dynamics, to create more comprehensive simulations.
By addressing these areas, the hybrid approach can continue to advance interior ballistics modeling and expand its applications in simulation-driven design and real-time ballistic solutions.
Conclusion
The hybrid approach combining physics-based simulations with machine learning has demonstrated significant potential in accurately predicting bullet velocities. The approach offers several advantages over traditional methods, including improved accuracy, increased efficiency, and flexibility. While there are limitations and future directions to consider, the approach has the potential to revolutionize interior ballistics modeling and its applications in various industries.
