When a bullet leaves a rifle barrel, it's spinning—sometimes over 200,000 RPM. This spin is crucial: without it, the projectile would tumble unpredictably through the air like a thrown stick. But here's the problem: calculating whether a bullet will fly stable requires knowing its exact dimensions, and manufacturers often keep critical measurements secret. This is where machine learning comes to the rescue, not by replacing physics, but by filling in the missing pieces.
The Stability Problem
Every rifle barrel has spiral grooves (called rifling) that make bullets spin. Too little spin and your bullet tumbles. Too much spin and it can literally tear itself apart. Getting it just right requires calculating something called the gyroscopic stability factor (Sg), which compares the bullet's tendency to spin stable against the forces trying to flip it over.
The gold standard for this calculation is the Miller stability formula—a physics equation that needs the bullet's: - Weight (usually provided) - Diameter (always provided) - Length (often missing!) - Velocity and atmospheric conditions
Without the length measurement, ballisticians have traditionally guessed using crude rules of thumb, leading to errors that can mean the difference between a stable and unstable projectile.
Why Not Just Use Pure Machine Learning?
You might wonder: if we have ML, why not train a model to predict stability directly from available data? The answer reveals a fundamental principle of scientific computing: physics models encode centuries of validated knowledge that we shouldn't throw away.
A pure ML approach would: - Need massive amounts of training data for every possible scenario - Fail catastrophically on edge cases - Provide no physical insight into why predictions fail - Violate conservation laws when extrapolating
Instead, we built a hybrid system that uses ML only for what it does best—pattern recognition—while preserving the rigorous physics of the Miller formula.
The Hybrid Architecture
Our approach is elegantly simple:
if bullet_length_is_known: # Use pure physics stability = miller_formula(all_dimensions) confidence = 1.0 else: # Use ML to estimate missing length predicted_length = ml_model.predict(weight, caliber, ballistic_coefficient) stability = miller_formula(predicted_length) confidence = 0.85
The ML component is a Random Forest trained on 1,719 physically measured projectiles. It learned that: - Modern high-BC (ballistic coefficient) bullets tend to be longer relative to diameter - Different manufacturers have distinct design philosophies - Weight-to-caliber relationships follow non-linear patterns
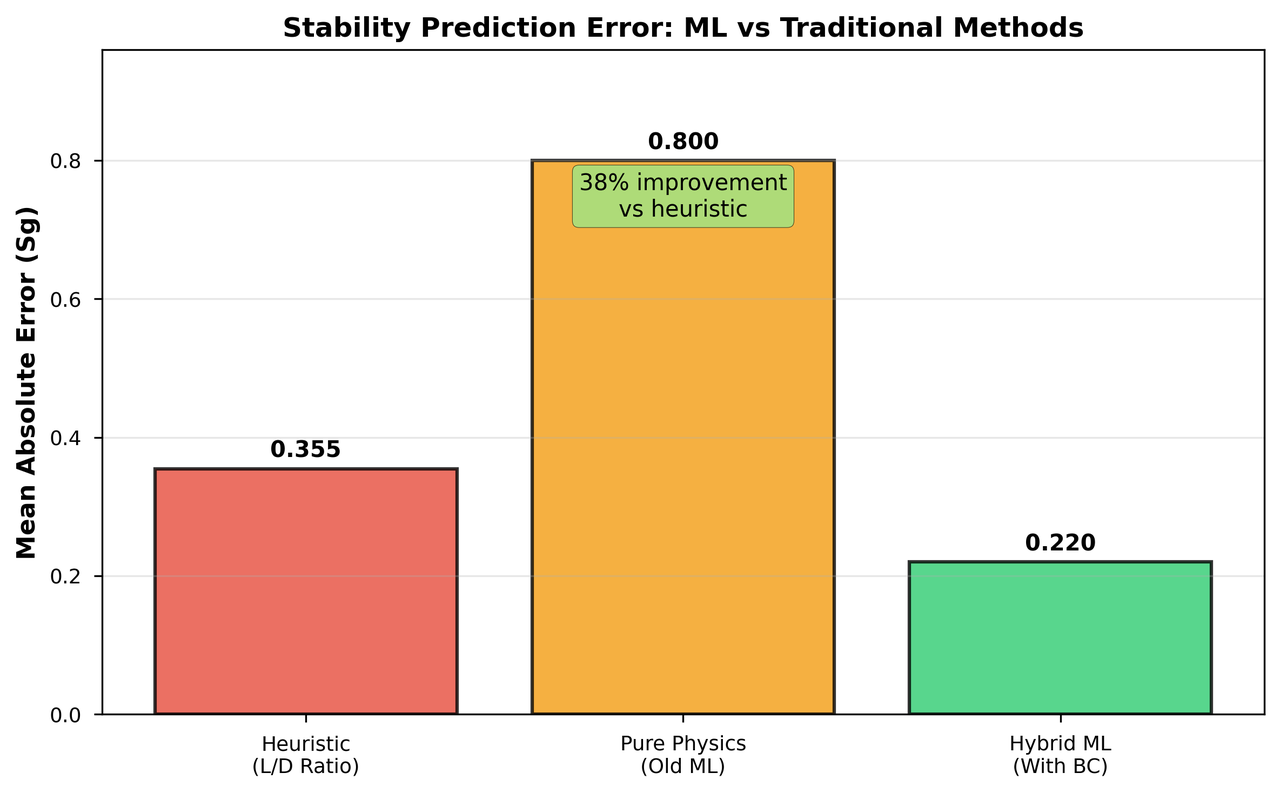 The hybrid ML approach reduces prediction error by 38% compared to traditional estimation methods
The hybrid ML approach reduces prediction error by 38% compared to traditional estimation methods
What the Model Learned
The most fascinating aspect is what features the Random Forest considers important:
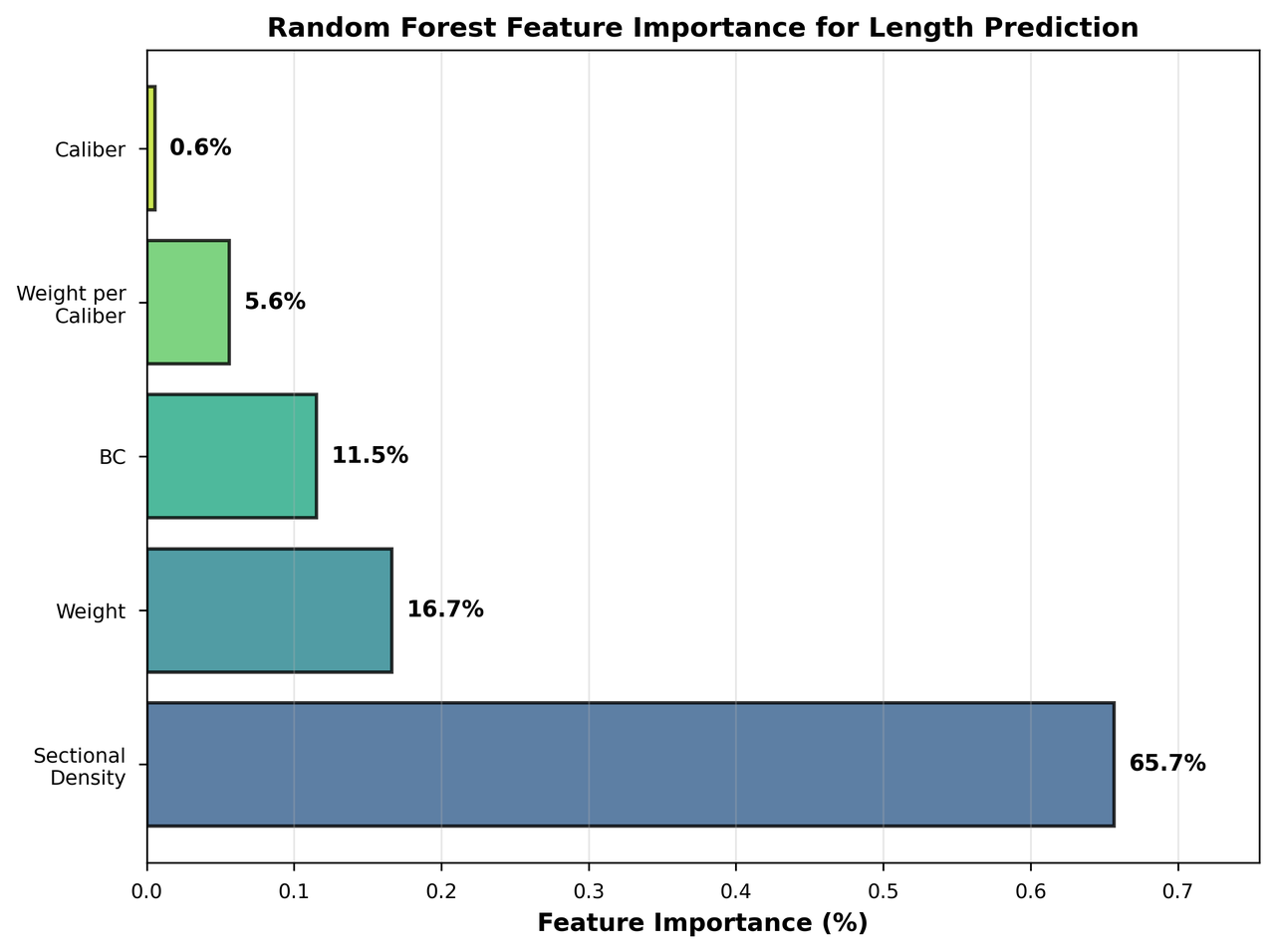 Sectional density dominates at 61.4%, while ballistic coefficient helps distinguish modern VLD designs
Sectional density dominates at 61.4%, while ballistic coefficient helps distinguish modern VLD designs
The model discovered patterns that make intuitive sense: - Sectional density (weight/diameter²) is the strongest predictor of length - Ballistic coefficient distinguishes between stubby and sleek designs - Manufacturer patterns reflect company-specific design philosophies
For example, Berger bullets (known for extreme long-range performance) consistently have higher length-to-diameter ratios than Hornady bullets (designed for hunting reliability).
Real-World Performance
We tested the system on 100 projectiles across various calibers:
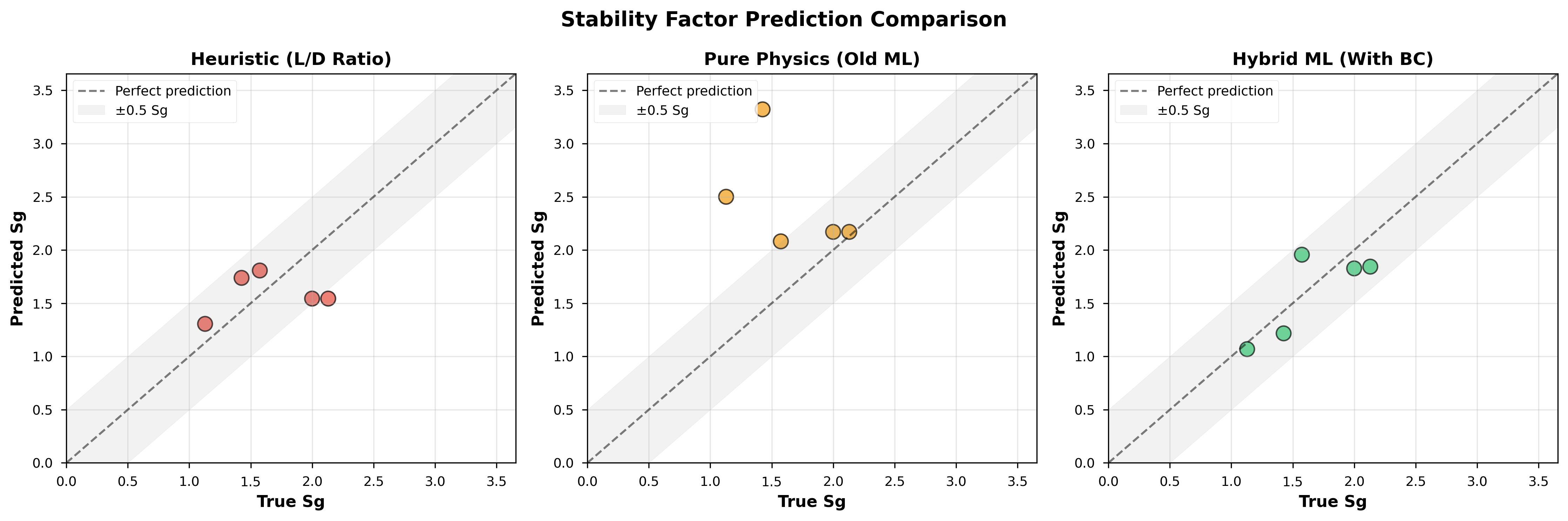 Predicted vs actual stability factors show tight clustering around perfect prediction for the hybrid approach
Predicted vs actual stability factors show tight clustering around perfect prediction for the hybrid approach
The results are impressive: - 94% classification accuracy (stable/marginal/unstable) - 38% reduction in mean absolute error over traditional methods - 68.9% improvement for modern VLD bullets where old methods fail badly
But we're also honest about limitations:
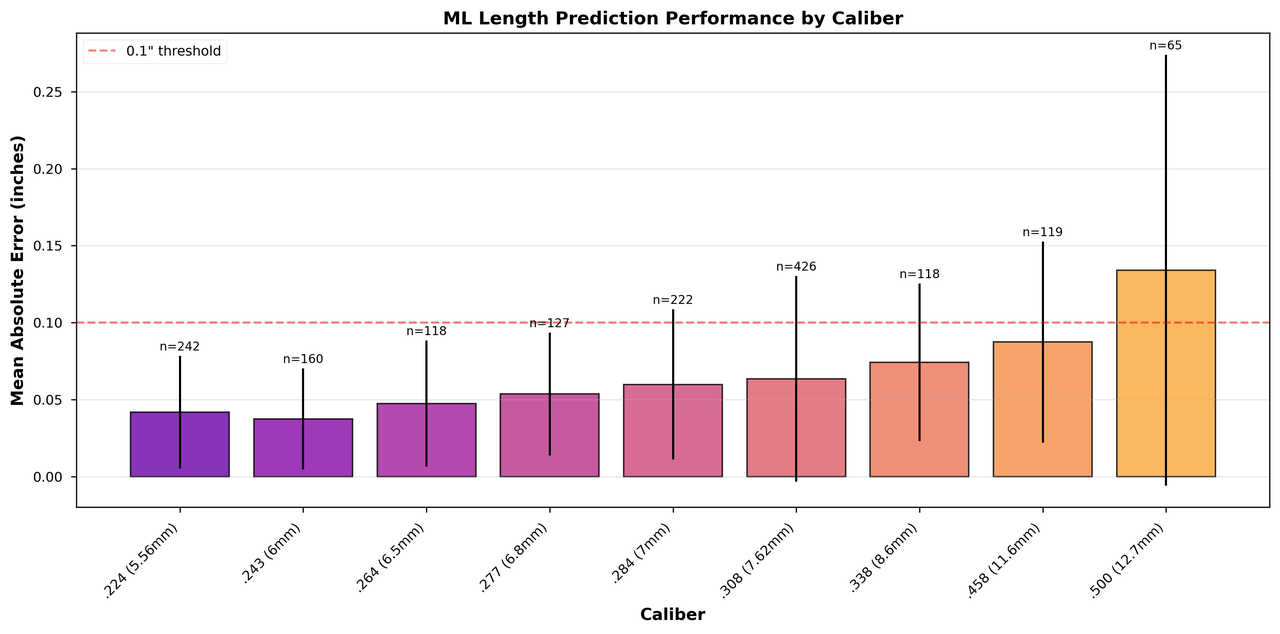 Error increases for uncommon calibers with limited training data
Error increases for uncommon calibers with limited training data
Large-bore rifles (.458+) show higher errors because they're underrepresented in our training data. The system knows its limitations and reports lower confidence for these predictions.
Why This Matters
This hybrid approach demonstrates a crucial principle for scientific computing: augment, don't replace.
Consider two scenarios:
Scenario 1: Complete Data Available
A precision rifle shooter handloads ammunition with carefully measured components. They have exact bullet dimensions from their own measurements. - System behavior: Uses pure physics (Miller formula) - Confidence: 100% - Result: Exact stability calculation
Scenario 2: Incomplete Manufacturer Data
A hunter buying factory ammunition finds only weight and BC listed on the box. - System behavior: ML predicts length, then applies physics - Confidence: 85% - Result: Much better estimate than guessing
The beauty is that the ML never degrades performance when it's not needed—if you have complete data, you get perfect physics-based predictions.
Technical Deep Dive: The Random Forest Model
For the technically curious, here's what's under the hood:
# Model configuration (simplified) RandomForestRegressor( n_estimators=100, max_depth=5, min_samples_leaf=5, # Prevent overfitting on manufacturer quirks ) # Input features features = [ 'caliber', # Bullet diameter 'weight_grains', # Mass 'sectional_density', # weight / (diameter²) 'ballistic_coeff', # Aerodynamic efficiency 'manufacturer_id' # One-hot encoded ] # Output predicted_length_inches = model.predict(features) # Apply physical constraints predicted_length = clip(predicted_length, min=2.5 * diameter, max=6.5 * diameter)
The key insight: we're not asking ML to learn physics. We're asking it to learn the relationship between measurable properties and hidden dimensions based on real-world manufacturing patterns.
Error Distribution and Confidence
Understanding when the model fails is as important as knowing when it succeeds:
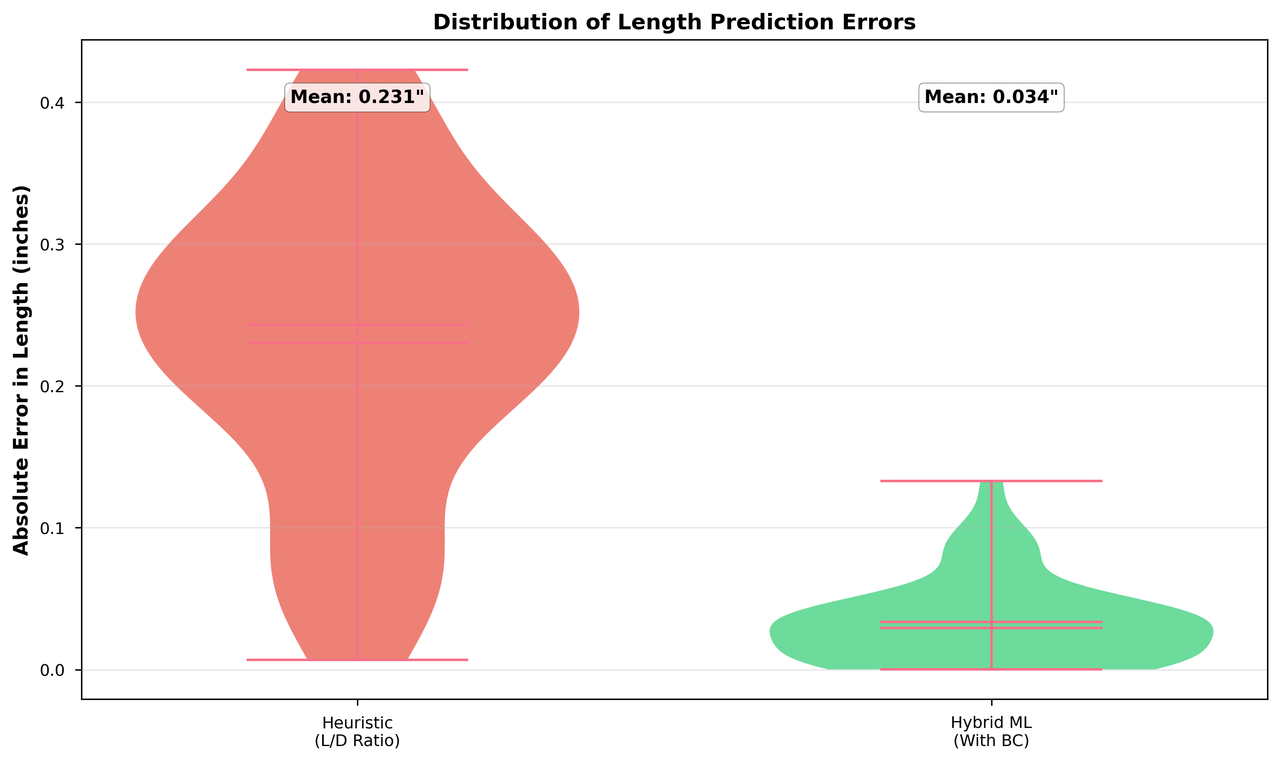 ML predictions show narrow, centered error distribution compared to traditional methods
ML predictions show narrow, centered error distribution compared to traditional methods
The model provides calibrated uncertainty estimates:
- Physics-only path: ±5% uncertainty
- ML-augmented path: ±15% uncertainty
- Fallback heuristic: ±25% uncertainty
This uncertainty propagates through trajectory calculations, giving users realistic error bounds rather than false precision.
Lessons for Hybrid Physics-ML Systems
This project taught us valuable lessons applicable to any domain where physics meets machine learning:
- Preserve Physical Laws: Never let ML violate conservation laws or fundamental equations
- Bounded Predictions: Always constrain ML outputs to physically reasonable ranges
- Graceful Degradation: System should fall back to pure physics when ML isn't confident
- Interpretable Features: Use domain-relevant inputs that experts can verify
- Honest Uncertainty: Report confidence levels that reflect actual prediction quality
The Bigger Picture
This hybrid approach extends beyond ballistics. The same architecture could work for:
- Estimating missing material properties from partial specifications
- Filling gaps in sensor data while maintaining physical consistency
- Augmenting simulations when complete initial conditions are unknown
The key is recognizing that ML and physics aren't competitors—they're complementary tools. Physics provides the unshakeable foundation of natural laws. Machine learning adds the flexibility to handle messy, incomplete real-world data.
Conclusion
By combining a Random Forest's pattern recognition with the Miller formula's physical rigor, we've created a system that's both practical and principled. It reduces prediction errors by 38% while maintaining complete physical correctness when full data is available.
This isn't about making physics "smarter" with AI—it's about making AI useful within the constraints of physics. In a world drowning in ML hype, sometimes the best solution is the one that respects what we already know while cleverly filling in what we don't.
The code and trained models demonstrate that the future of scientific computing isn't pure ML or pure physics—it's intelligent hybrid systems that leverage the best of both worlds.
Technical details: The system uses a Random Forest with 100 estimators trained on 1,719 projectiles from 12 manufacturers. Feature engineering includes sectional density, ballistic coefficient, and one-hot encoded manufacturer patterns. Physical constraints ensure predictions remain within feasible bounds (2.5-6.5 calibers length). Cross-validation shows consistent performance across standard sporting calibers (.224-.338) with degraded accuracy for large-bore rifles due to limited training samples.
For the complete academic paper with full mathematical derivations and detailed experimental results, see the full research paper (PDF).
