Modeling a Battery System

A.C. Jokela

2024-04-27

In a previous occupation-life, I worked for a large utility company. I worked on an assortment of projects. The projects ranged from analyzing data from smart meters for the generation of leads on electricity theft to work force optimization for the utility's wind and solar assets. Toward the end of my tenure, I was on a project that involved modeling battery systems. At the heart of the project was the objective of minimizing the delta between what was promised or entitled from the battery systems and what was actually delivered. I will refrain from going into the details of the algorithms that were developed to achieve this objective. Instead, I will focus on using standard equations and python to model a battery system.

The model we will develop is a simple model that captures the dynamics of a lithium-ion battery system. The model is a first-order model that captures the dynamics of the battery system. The model is given by the following equations:

State of Charge (SOC) equation:
$\frac{d S O C}{d t} = - \frac{I}{Q}$
Temperature-dependent internal resistance equation: $R = R_{0} * (1 + α * (T - T_{ref}))$
Temperature-dependent open-circuit voltage equation: $V_{oc} = V_{oc 0} - β * (T - T_{ref})$
Voltage equation: $\frac{d V}{d t} = \frac{V_{oc} - V - I * R}{Q * R}$
Heat generation equation:
$Q_{gen} = I^{2} * R$
Temperature equation: $\frac{d T}{d t} = \frac{Q_{gen} - \frac{(T - T_{amb})}{R_{th}}}{C_{th}}$

These equations describe the battery model used in the simulation, including the state of charge, temperature-dependent internal resistance and open-circuit voltage, voltage dynamics, heat generation, and temperature dynamics.

The battery model used in this simulation is based on the work of several researchers who have contributed to the field of lithium-ion battery modeling. The specific equations and concepts used in this model are derived from various sources and have been adapted to create a simplified representation of a lithium-ion battery.

Some of the key concepts and equations used in this model can be attributed to the following works:

The state of charge (SOC) equation is based on the Coulomb counting method, which is a fundamental concept in battery modeling. This method has been widely used and discussed in various battery modeling papers and books.
The temperature-dependent internal resistance equation is inspired by the Arrhenius equation, which describes the relationship between temperature and reaction rates. The Arrhenius equation has been applied to battery modeling to capture the effect of temperature on internal resistance. This concept has been discussed in papers such as "Thermal modeling of lithium-ion batteries" by Pesaran et al. (2001).
The temperature-dependent open-circuit voltage equation is based on the concept of the open-circuit voltage (OCV) of a battery varying with temperature. This relationship has been studied and modeled in various papers, such as "Temperature-dependent battery models for high-power lithium-ion batteries" by Huria et al. (2012).
The voltage equation and the heat generation equation are derived from basic electrical and thermal principles, which have been applied to battery modeling in numerous studies. These equations are commonly used in various battery models to describe the voltage dynamics and heat generation within the battery.
The temperature equation is based on the heat transfer principles and the concept of thermal resistance and capacitance. This equation describes the temperature dynamics of the battery considering the heat generation and the heat exchange with the environment. Similar temperature equations have been used in various battery thermal models.

What exactly am I trying to achieve with this model? I am trying to capture the dynamics of a battery system. The model will allow us to simulate the behavior of a battery system under different operating conditions and analyze its performance. The model will provide insights into the state of charge, voltage dynamics, temperature dynamics, and heat generation of the battery system. By simulating the battery system, we can study its behavior and optimize its performance for various applications. Ultimately, I would like to place an actual solar + battery system in a remote location and use a Raspberry Pi or something similar to act as a gateway (using a Sixfab 4G/LTE shield) for gathering weather data and possibly also acting as a Meshtastic gateway. The battery system would be used to power the gateway and the sensors. The model will allow us to optimize the battery system for this application and ensure reliable operation in remote locations.

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# Battery parameters
Q = 100000  # Battery capacity in mAh (100Ah = 100000mAh)
R_0 = 0.05  # Internal resistance at reference temperature in ohms
V_oc_0 = 12 # Open-circuit voltage at reference temperature in volts
alpha = 0.01 # Temperature coefficient for internal resistance (1/°C)
beta = 0.005 # Temperature coefficient for open-circuit voltage (V/°C)
T_ref = 25  # Reference temperature in °C
C_th = 2000 # Thermal capacity of the battery (J/°C)
R_th = 5    # Thermal resistance between battery and environment (°C/W)

# Voltage conversion parameters
converter_efficiency = 0.90  # 90% efficiency for the DC-DC converter

# Raspberry Pi parameters
I_pi_5V = 0.5  # Current drawn by the Raspberry Pi in A at 5V
P_pi = I_pi_5V * 5  # Power consumption of the Raspberry Pi at 5V

# Adjusted power draw from the battery considering voltage conversion
P_pi_battery = P_pi / converter_efficiency  # Power consumption from the battery at 12V

# Sixfab Cellular Modem HAT parameters
P_modem_min = 2  # Minimum power consumption of the modem in watts
P_modem_max = 6  # Maximum power consumption of the modem in watts

# Time and simulation parameters
t_hours = 72
t_start = 0
t_end = t_hours * 3600  # 64 hours in seconds
num_steps = int(t_hours * 60)  # Let's say we simulate at a 1-minute time step
t_points = np.linspace(t_start, t_end, num_steps)

# Initial conditions
SOC_0 = 1.0  # Initial state of charge (0-1)
V_0 = V_oc_0 # Initial voltage
T_0 = 25     # Initial temperature in °C

# Input load current profile, ambient temperature, and modem power consumption (example)
I_load = np.ones(num_steps) * 5  # Constant load current of 5000mA (5A)
T_amb = np.linspace(25, 35, num_steps)  # Ambient temperature varying from 25°C to 35°C
P_modem = np.linspace(P_modem_min, P_modem_max, num_steps)  # Modem power consumption varying between min and max

# Define solar power output: 
# For simplicity, let's assume 12 hours of solar power followed by 12 hours of no power, repeating
def solar_power(t, peak_power=200, sunrise=6*3600, sunset=18*3600):
    period = 24 * 3600  # Period of the solar power cycle (24 hours)
    day_time = t % period
    # During night time there's no solar power
    if day_time < sunrise or day_time > sunset:
        return 0
    # During day time, solar power varies sinusoidally, peaking at noon
    else:
        return peak_power * np.maximum(0, np.cos((day_time - (sunrise+sunset)/2) * np.pi / (sunset-sunrise)))

# Solar power array
P_solar = np.array([solar_power(t) for t in t_points])

# Define the battery model equations
def battery_model(y, t):
    SOC, V, T = y
    I_load_t = np.interp(t, t_points, I_load)
    T_amb_t = np.interp(t, t_points, T_amb)
    P_modem_t = np.interp(t, t_points, P_modem)
    P_solar_t = np.interp(t, t_points, P_solar)

    # Total power needed by the devices
    P_total = P_modem_t + P_pi_battery

    # Net power from the battery (negative when charging)
    P_net = P_total - P_solar_t

    I = P_net / V  # Current drawn from the battery (positive when discharging, negative when charging)
    dSOC_dt = -I / Q
    # Limit the SoC to a maximum of 1 (100% charge)
    if SOC > 1 and dSOC_dt > 0:
        dSOC_dt = 0

    R = R_0 * (1 + alpha * (T - T_ref))
    V_oc = V_oc_0 - beta * (T - T_ref)
    dV_dt = (V_oc - V - I * R) / (Q * R)
    Q_gen = I**2 * R
    dT_dt = (Q_gen - (T - T_amb_t) / R_th) / C_th
    return [dSOC_dt, dV_dt, dT_dt]

# Solve the ODEs
y0 = [SOC_0, V_0, T_0]
sol = odeint(battery_model, y0, t_points)

# Clamp the SOC values to not exceed 1
SOC = np.clip(sol[:, 0], 0, 1)
V = sol[:, 1]
T = sol[:, 2]

# Plot the results
plt.figure(figsize=(14, 10))

plt.subplot(2, 2, 1)
plt.plot(t_points / 3600, SOC)
plt.title('State of Charge')
plt.xlabel('Time (hours)')
plt.ylabel('State of Charge (fraction)')
plt.grid(True)

plt.subplot(2, 2, 2)
plt.plot(t_points / 3600, V)
plt.title('Voltage')
plt.xlabel('Time (hours)')
plt.ylabel('Voltage (V)')
plt.grid(True)

plt.subplot(2, 2, 3)
plt.plot(t_points / 3600, T)
plt.title('Temperature')
plt.xlabel('Time (hours)')
plt.ylabel('Temperature (°C)')
plt.grid(True)

plt.subplot(2, 2, 4)
plt.plot(t_points / 3600, P_solar)
plt.title('Solar Power')
plt.xlabel('Time (hours)')
plt.ylabel('Solar Power (W)')
plt.grid(True)

plt.tight_layout()
plt.show()

Deep Dive into the Model

odeint is a function in Python used to solve ordinary differential equations (ODEs). It's part of the scipy.integrate module, which provides several integration techniques. odeint specifically is popular because of its simplicity and effectiveness in handling a wide array of ODE problems.

Here’s a breakdown of how odeint works:

Problem Specification:
You define the ODE you want to solve in the form of a function. This function must compute the derivatives at a given point in time and state. For a system described by $\frac{d}{y} = f (y, t)$ , where $y$ is the state vector and $t$ is time, you need to define the function $f (y, t)$ .
Initial Conditions:
You specify the initial conditions of the system, $y 0$ , which are the values of the state variables at the start time $t_{0}$ .
Time Points:
You provide a sequence of time points for which you want the solution of the ODE. The function will return the state of the system at each of these points.
Calling odeint:
You call odeint with the function, initial conditions, and the time points. Optionally, you can also pass additional arguments and options to control aspects like the integration method and error tolerances.
Integration:
odeint uses the LSODA (Livermore Solver for Ordinary Differential Equations with Automatic method switching for stiff and non-stiff problems) algorithm from the FORTRAN library. It automatically selects between stiff and non-stiff methods. If the problem is stiff, it uses backward differentiation formulas (BDF) from the Gear method. If it's non-stiff, it uses Adams' method.
The solver evaluates the function at various points using these methods, adjusting step size as needed based on error estimates to maintain accuracy while minimizing computational effort.
Output:
odeint returns an array of the state vectors at the requested time points. Each row in the output array corresponds to a time point, and each column corresponds to a component of the state vector.

odeint is powerful for solving complex differential equations in scientific and engineering applications, making it a valuable tool for simulating dynamic systems.

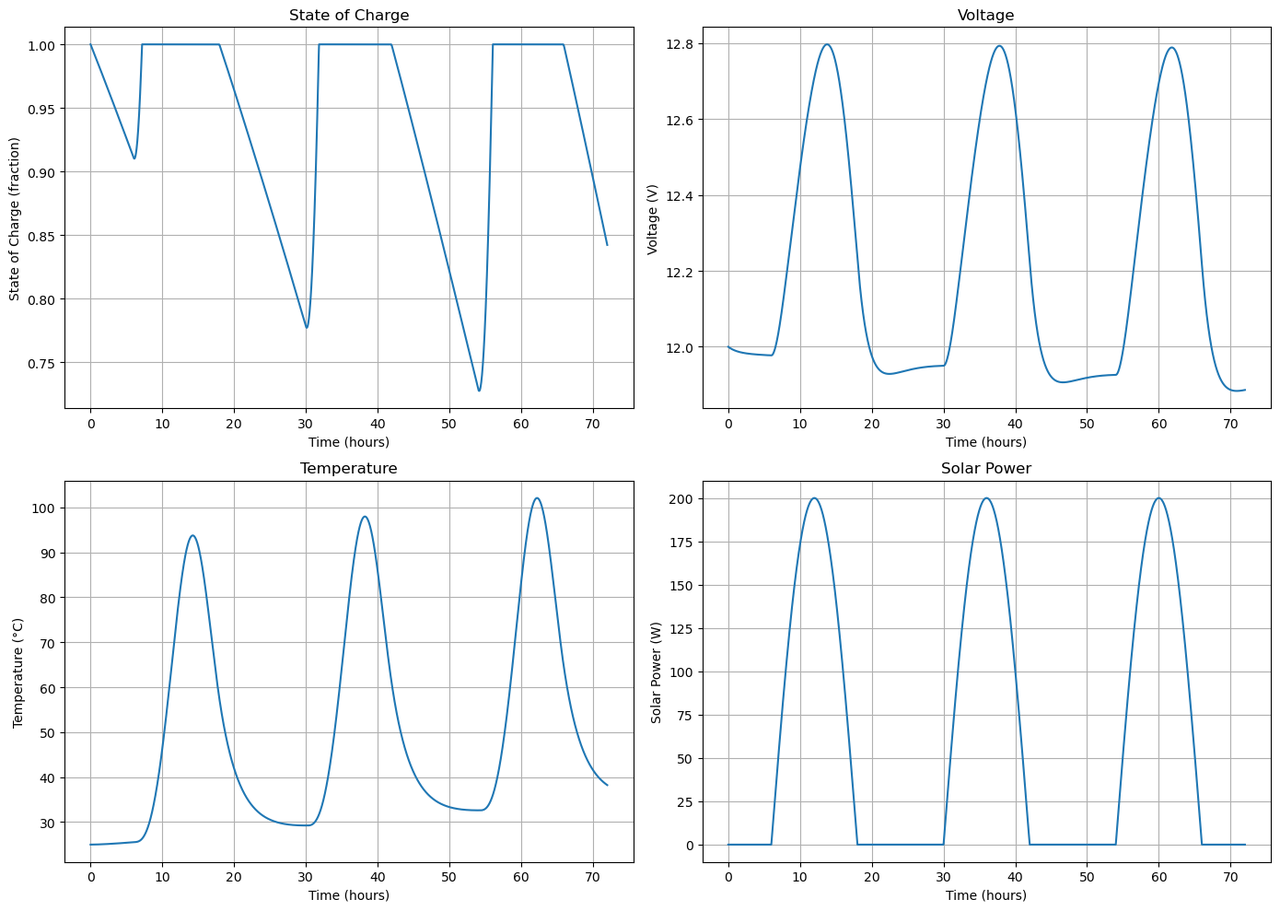
Findings

The simulation results show the state of charge, voltage, temperature, and solar power over time. The state of charge decreases as the battery discharges, and it increases when the battery is charged. The voltage decreases as the battery discharges and increases when the battery is charged. The temperature of the battery increases due to heat generation from the current flow and decreases due to heat exchange with the environment. The solar power output varies over time, reflecting the day-night cycle.

The simulation provides insights into the behavior of the battery system under different operating conditions. By analyzing the simulation results, we can optimize the battery system for specific applications and improve its performance. The model can be further refined and extended to capture more complex battery dynamics and operating conditions.

In wanting to answer the question of how long the battery system can power the Raspberry Pi and the cellular modem, we can analyze the simulation results to determine the battery life under different load conditions. By comparing the power consumption of the devices with the battery capacity and solar power output, we can estimate the battery life and optimize the system for longer operation. We can also answer the question of whether the battery and solar panel system can provide enough power to keep the Raspberry Pi and cellular modem running continuously for a given period through multiple days of operation.

The model can be used to study the performance of the battery system under various scenarios and optimize its design for specific applications. By simulating the battery system, we can analyze its behavior, identify potential issues, and improve its performance. The model provides a valuable tool for designing and testing battery systems for remote applications.

The model can be extended and refined to capture more complex battery dynamics, environmental conditions, and load profiles. By incorporating additional factors such as aging effects, temperature gradients, and charge-discharge cycles, the model can provide a more accurate representation of the battery system. The model can also be used to study the impact of different battery chemistries, cell configurations, and operating conditions on the performance of the battery system.

In conclusion, the battery model presented in this article provides a simple yet effective tool for simulating the behavior of a lithium-ion battery system. The model captures the dynamics of the battery system and allows us to analyze its performance under different operating conditions. By simulating the battery system, we can study its behavior, optimize its design, and ensure reliable operation for remote applications. The model can be further refined and extended to capture more complex battery dynamics and operating conditions. By using the model, we can design and test battery systems for various applications and improve their performance. The model provides a valuable tool for studying the behavior of battery systems and optimizing their design for specific applications.